Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔEAC và ΔBAD có :
AD = AC ( gt )
ˆCAE=ˆDAB( hai góc đối đỉnh )
AE = AB ( gt )
nên ΔEAC=ΔBAD(c.g.c)
=> BD = CE ( hai cạnh tương ứng )


Lấy điểm M thuộc tia AM sao cho M là trung điểm của AM.
Ta chứng minh được:
\(\Delta AMB=\Delta M'MC\left(c.g.c\right)\) suy ra AB = BM'.
\(\Delta AMC=\Delta M'MB\left(c.g.c\right)\Rightarrow AC=BM'\), \(\widehat{CAM}=\widehat{BM'M}\).
Theo định lý tổng ba góc trong tam giác:
\(\widehat{M'AB}+\widehat{BM'A}+\widehat{ABM'}=180^o\Leftrightarrow\widehat{BAM'}+\widehat{ABM'}+\widehat{M'AC}=180^o\).
Mà \(\widehat{DAE}+\widehat{BAM}+\widehat{MAC}=180^o\).
Suy ra \(\widehat{DAE}=\widehat{ABM'}\).
Xét tam giác DAE và tam giác ABM' cóL
DA = AB.
BM' = AC = AE.
\(\widehat{DAE}=\widehat{ABM'}\).
Suy ra \(\Delta DAE=\Delta AB'M\left(c.g.c\right)\).
Suy ra DM = AM' = 2AM. (đpcm).

a) Xét ∆AEB và ∆ADC ta có :
EA = AC
DA = AB
EAB = DAC( 2 góc đối đỉnh)
=> ∆AEB = ∆ADC (c.g.c)(dpcm)
=> BE = DC ( 2 cạnh tương ứng) (dpcm)
a)
có \(\widehat{DAC}=90^0+\widehat{BAC}\) ; \(\widehat{BAE}=90^0+\widehat{BAC}\)
\(\Rightarrow\widehat{DAC}=\widehat{BAE}\)
Xét \(\Delta ADC\)và \(\Delta ABE\)
có \(\widehat{DAC}=\widehat{BAE}\)
\(AB=AD\)
\(AC=AE\)
nên \(\Delta ADC=\text{}\Delta ABE\left(c-g-c\right)\)
b)
có\(\Delta ADC=\text{}\Delta ABE\)
nên \(CD=BE\)

a) Trên tia đối tia MA lấy điểm F sao cho AM = AF (*)
Xét tam giác BFM và tam giác ACM có:
AM = FM (theo *)
Góc BMF = góc AMC (2 góc đối đỉnh)
BM = CM (vì M là trung điểm của BC)
=> Tam giác BFM = tam giác CAM (c.g.c)
=> AC = BF (2 cạnh tương ứng)
Vì AC = AE (gt) nên AE = BF
Ta có: góc F = góc CAM (vì tam giác BFM = tam giác CAM)
Mà 2 góc này ở vị trí so le trong
=> BF // AC (dấu hiệu nhận biết)
=> Góc BAC + góc ABF = 180 độ (2 góc trong cùng phía)
Mà góc BAC + góc DAE = 180 độ
=> Góc DAE = góc ABF
Xét tam giác ABF và tam giác ADE có:
AB = AD (gt)
Góc DAE = góc ABF (chứng minh trên)
AE = BF (2 cạnh tương ứng)
=> Tam giác ADE = tam giác BAF (c.g.c)
=> AF = DE (2 cạnh tương ứng)
Lại có: AM = AF : 2 => AM = DE : 2 (đpcm)
b) Gọi giao điểm của AM và DE là N
Ta có: tam giác ADE = tam giác BAF (chứng minh trên)
=> Góc D = góc BAF (2 góc tương ứng)
Mà góc BAF + góc DAN = 180 độ - góc BAD = 180 độ - 90 độ = 90 độ
=> Góc D + góc DAN = 90 độ
=> Tam giác ADN vuông tại N
hay AM _|_ DE (đpcm)
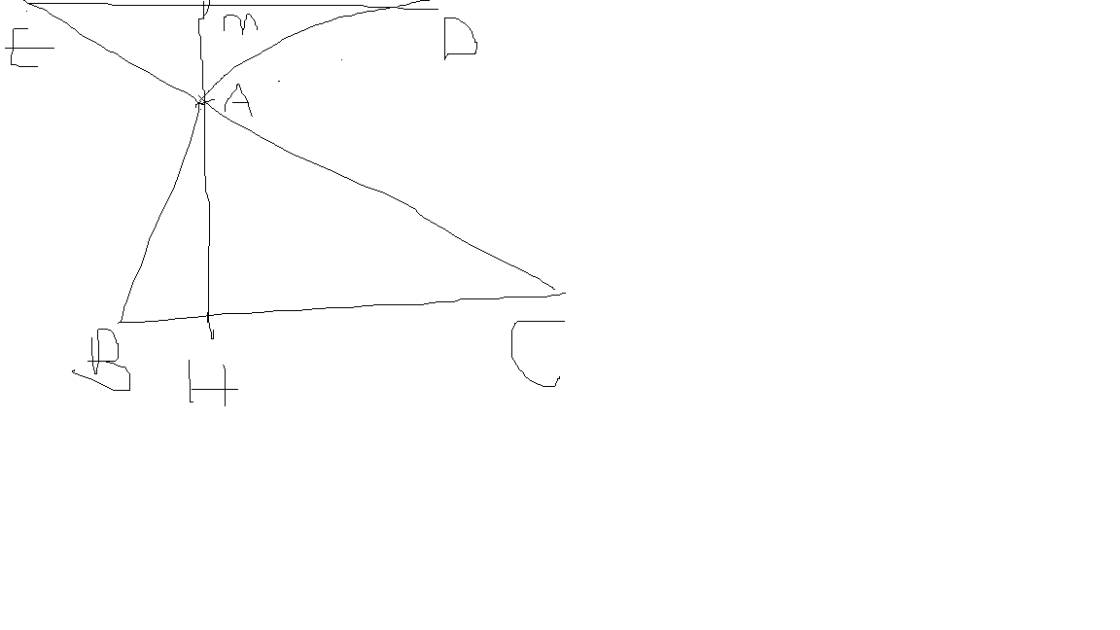
Xét \(\Delta EAC\) và \(\Delta BAD\) có :
AD = AC ( gt )
\(\widehat{CAE}=\widehat{DAB}\)( hai góc đối đỉnh )
AE = AB ( gt )
nên \(\Delta EAC=\Delta BAD\left(c.g.c\right)\)
=> BD = CE ( hai cạnh tương ứng )