một vật dao động điều hào với pt x=4cos(\(4\pi t+\dfrac{\pi}{6}\)) (cm) vật qua vị trí có li độ x=2cm lần thứ 2013 vào thời điểm bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
29 tháng 7 2023
Ta có: \(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\dfrac{2\pi}{3}}=3\left(s\right)\)
Thời gian vật đi từ vị trí có li độ x = 4 cm đến vị trí có li độ x = -2 lần đầu tiên là:
\(t_1=\dfrac{T}{4}+\dfrac{T}{12}=\dfrac{3}{4}+\dfrac{3}{12}=1\left(s\right)\)
Thời gian vật đi qua vị trí có li độ x = -2 lần thứ 2 đến vị trí có li độ x = -2 lần thứ 2011 là:
\(t_2=1005\cdot T=1005\cdot3=3015\left(s\right)\)
Tổng thời gian cần là: \(t=t_1+t_2=1+3015=3016\left(s\right)\)
17 tháng 7 2021
Khi t = 0, ban đầu vật ở vị trí x = 2 cm, di chuyển ngược chiều dương
Khi x = 2√3 cm thì cung Δφ = \(\dfrac{\text{7π}}{\text{6}}\)
=> Δt = \(\dfrac{\text{Δ}\text{φ}}{\text{ω}}\)= \(\dfrac{\text{7}}{\text{3}}\)s
Bạn vẽ vòng tròn lượng giác ra cho dễ làm hơn nha
17 tháng 7 2021
Hình như đề phải là x = 4cos(0.5π.t - \(\dfrac{\text{π}}{\text{3}}\)) cm chứ bạn
KA
22 tháng 6 2019
khi t=0 có x0=2\(\sqrt{3}\) cm
T=2π/ω=2 s
sử dụng đường tròn tính được thời gian vật đi qua vị trí cách vị trí cân bằng lần 1 là (nếu bạn không biết vẽ có thể hỏi mình)
t1=T/4
thời gian vật qua vị trí cách vị trí cân bằng 2 cm lần thứ 2013=1+503.4 là
t2013=t1+503.T=T/4 +503T =2013/2 s
13 tháng 8 2019
Ta có chu kì dao động là: T = \(\frac{2.\pi}{\omega}\) = 3s
Trong 1 chu kì vật qua vị trí x = -2 là 2 lần
⇒ Trong 1007 chu kì vật qua vị trí x = -2 là 2014 lần
Vậy khoảng thời gian vật qua vị trí x = -2 lần thứ 2014 là :
t = \(\left(\frac{T}{4}+\frac{T}{12}\right)\)+ 1007.3 = 3022s
2
28 tháng 9 2023
Thời điểm thứ hai vật đi qua li độ `x=5 cm` là: `\Delta t=[3T]/4+T/12=[5T]/6 (s)`
Thời điểm vật đi qua vị trí có li độ `x=5 cm` lần thứ `2008` là:
`t=[5T]/6+[2008-2]/2 T=6023/6 T=6023/6 . [2\pi]/[10\pi]=6023/30~~200,8(s)`.
M
18 tháng 8 2023
Để tính quảng đường và số lần vật qua vị trí x = -2cm trong khoảng thời gian từ t1 = 0.25s đến t2 = 2.125s, chúng ta cần tìm giá trị của t khi vị trí x bằng -2cm.
Theo phương trình x = 4cos(4πt + x/4), ta có: 4cos(4πt + x/4) = -2 cos(4πt + x/4) = -1/2
Để tìm giá trị của t, ta sử dụng hàm nghịch đảo của hàm cos: 4πt + x/4 = π + 2kπ hoặc 4πt + x/4 = 2π - 2kπ, với k là số nguyên.
Giải phương trình đầu tiên: 4πt + x/4 = π + 2kπ 4πt = π + 2kπ - x/4 t = (π + 2kπ - x/4) / (4π)
Giải phương trình thứ hai: 4πt + x/4 = 2π - 2kπ 4πt = 2π - 2kπ - x/4 t = (2π - 2kπ - x/4) / (4π)
Từ đây, ta có thể tính giá trị của t bằng cách thay x = -2cm, kết hợp với giá trị của k từ t1 đến t2:
t1 = (π + 2kπ + 2/4) / (4π) t2 = (2π - 2kπ + 2/4) / (4π)
Từ đó, ta tính được quảng đường vật đi được: S1 = 4cos(4πt1 + x/4) S2 = 4cos(4πt2 + x/4)
Vậy, quảng đường và số lần vật qua vị trí x = -2cm từ t1=0.25s đến t2=2.125s là S2 - S1 và số lần vật qua vị trí x = -2cm sẽ là số k thỏa mãn trong khoảng từ t1 đến t2
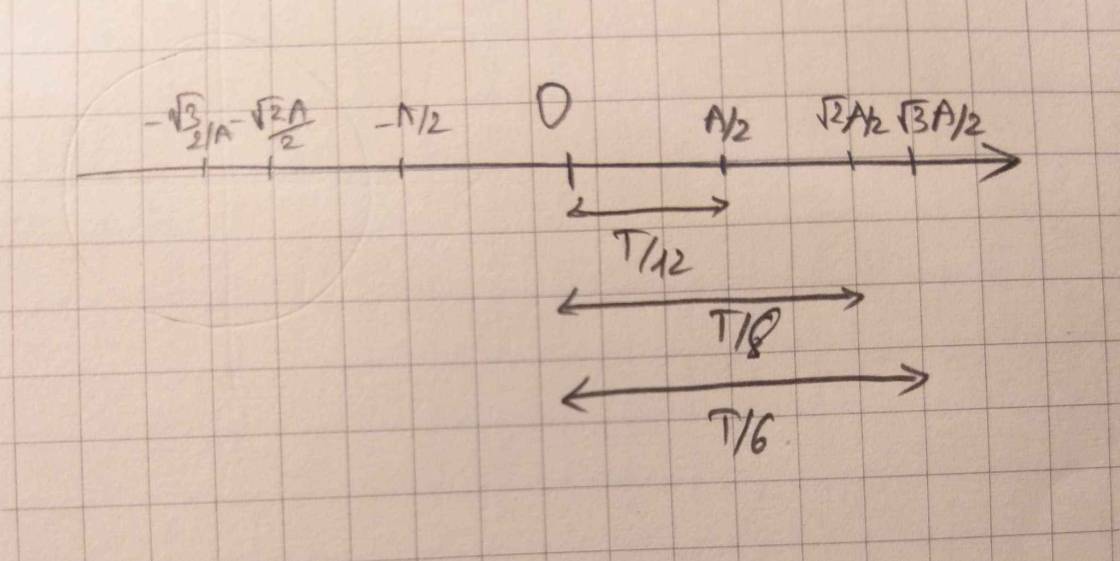
Do ban đầu vật ở vị trí có pha là \(\dfrac{\pi}{6}\)
⇒ Thời gian để vật đi qua vị trí có li độ x = 2 cm lần thứ nhất là
\(\dfrac{T}{12}=\dfrac{2\pi}{12w}=\dfrac{2\pi}{12\cdot4\pi}=\dfrac{1}{24}\left(s\right)\)
Thời gian để vật đi qua vị trí có li độ x = 2 cm lần thứ 2 đến lần thứ 2013 là
\(\dfrac{2012}{2}\cdot T=\dfrac{2012}{2}\cdot\dfrac{1}{2}=503\left(s\right)\)
Vậy tổng thời gian là \(503+\dfrac{1}{24}\simeq503,042\left(s\right)\)