Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\dfrac{2\pi}{3}}=3\left(s\right)\)
Thời gian vật đi từ vị trí có li độ x = 4 cm đến vị trí có li độ x = -2 lần đầu tiên là:
\(t_1=\dfrac{T}{4}+\dfrac{T}{12}=\dfrac{3}{4}+\dfrac{3}{12}=1\left(s\right)\)
Thời gian vật đi qua vị trí có li độ x = -2 lần thứ 2 đến vị trí có li độ x = -2 lần thứ 2011 là:
\(t_2=1005\cdot T=1005\cdot3=3015\left(s\right)\)
Tổng thời gian cần là: \(t=t_1+t_2=1+3015=3016\left(s\right)\)

Phương trình dạo động là: \(x=4cos\left(2\pi t+\dfrac{\pi}{3}\right)cm\)
Chu kì dao động là: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{2\pi}=1\left(s\right)\Rightarrow0,25=\dfrac{T}{4}\)
Tại thời điểm t1, vật có li độ đang giảm và có giá trị 2cm
\(\Rightarrow\Delta\varphi=\dfrac{\pi}{3}\)
Tại thời điểm t2 = t1 + 0,25, vật quay một góc \(\dfrac{\pi}{2}\) so với thời điểm t1.
\(\Rightarrow x_2=-\dfrac{A\sqrt{3}}{2}=-\dfrac{4\sqrt{3}}{2}=-2\sqrt{3}\left(cm\right)\)
Chọn A.

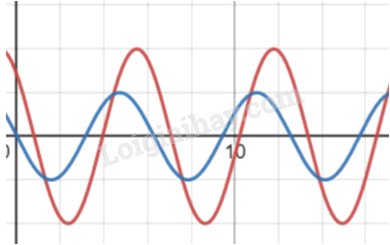
Dao động 1 vẽ với biên độ A và chu kì T
Dao động 2 có cùng chu kì với dao động 1 và biên độ \(A_2=2A\) vị trí đầu tiên của dao động thứ hai bằng \(\dfrac{\sqrt{2}}{2}A_2\) và ở thời điểm \(\dfrac{T}{8}\) thì dao động 2 sẽ đi qua vị trí cân bằng.
Cứ thế tiếp tục vẽ 2 chu kì dao động của hai dao động
Đường màu xanh là dao động thứ nhất, đường màu đỏ là dao động thứ 2

`a)A=4 (cm)`
`\omega=2\pi .f=10\pi (rad//s)`
Tại `t=0` thì `x_0 =-4=>\varphi=\pi (rad)`
`=>` Ptr: `x=4cos(10\pi t+\pi)`.
`b)` Ta có: `t=T/4 -T/6=T/12 =1/12 . [2\pi]/[10\pi]=1/60 (s)`
`c)T=[2\pi]/[10\pi]=0,2(s)`
`=>` Trong `2s` vật đi được `t=2/[0,2]=10T`
`=>` Quãng đường đi được trong `2s` là: `s=10.4.A=160(cm)`.
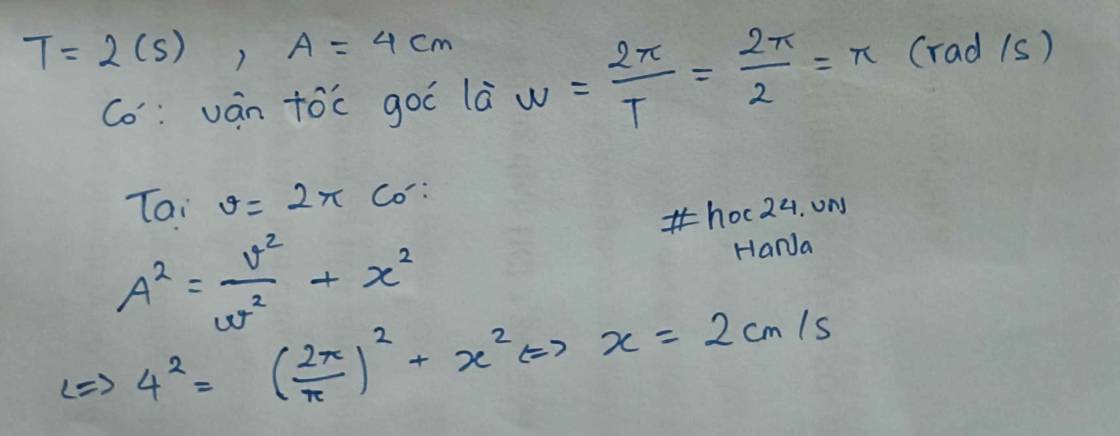
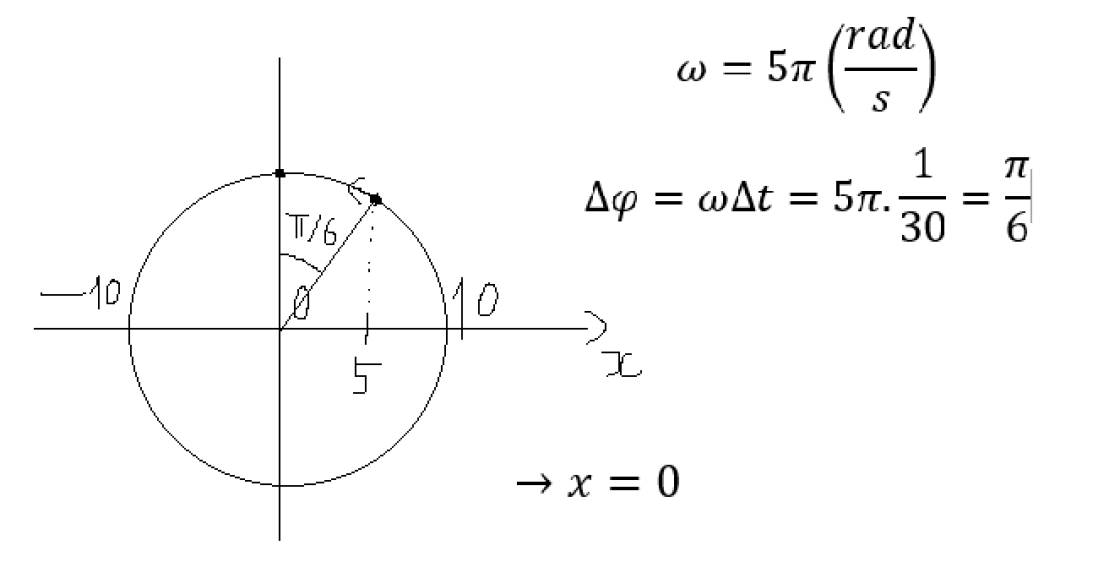
Do ban đầu vật ở vị trí có pha là \(\dfrac{\pi}{6}\)
⇒ Thời gian để vật đi qua vị trí có li độ x = 2 cm lần thứ nhất là
\(\dfrac{T}{12}=\dfrac{2\pi}{12w}=\dfrac{2\pi}{12\cdot4\pi}=\dfrac{1}{24}\left(s\right)\)
Thời gian để vật đi qua vị trí có li độ x = 2 cm lần thứ 2 đến lần thứ 2013 là
\(\dfrac{2012}{2}\cdot T=\dfrac{2012}{2}\cdot\dfrac{1}{2}=503\left(s\right)\)
Vậy tổng thời gian là \(503+\dfrac{1}{24}\simeq503,042\left(s\right)\)