cho tứ giác ABCD nội tiếp .Gọi I là giao điểm của AC và BD .Kẻ IH vuông góc AB , IK vuông góc AD
a, CMR tứ giác AHIK nội tiếp
b, CMR IA*IC=IB*ID
c, CMR tam giác HIK và tam giác BCD đồng dạng
d, Gọi S là diện tích tam giác ABD ,S' là diện tích tam giác HIK . CMR \(\frac{s}{s'}\)\(\le\)\(\frac{HK^2}{4\cdot AI^2}\)
các bạn giúp mk lẹ lẹ nha mk đag cần lời giải gấp

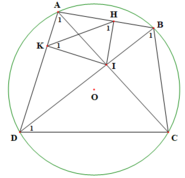
a/ Ta có
IH vuông góc AB => ^AHI = 90
IK vuông góc AD => ^AKI = 90
=> H và K cùng nhìn AI dưới hai góc bằng nhau => AHIK là tứ giác nội tiếp
b/ Xét tam giác ADI và tam giác BCI có
^AID=^BIC (góc đối đỉnh)
sđ ^DAC = sđ ^DBC = 1/2 sđ cung CD (góc nội tiếp) => ^DAC=^DBC
=> tg ADI đồng dạng tg BCI
=> \(\frac{IA}{IB}=\frac{ID}{IC}\Rightarrow IA.IC=IB.ID\)
c/
Xét tứ giác nội tiếp AHIK có
^HIK = 180 - ^DAB (hai góc đối của tứ giác nội tiếp bù nhau) (1)
^DAC = ^KHI (2 góc nội tiếp chắn cùng 1 cung) (2)
Xét tứ giác nội tiếp ABCD có
^BCD = 180 - ^DAB (hai góc đối của tứ giác nội tiếp bù nhau) (3)
^DAC = ^DBC (hai góc nội tiếp chắn cùng 1 cung) (4)
Xét hai tam giác HIK và tam giác BCD
Từ (1) và (3) => ^HIK = ^BCD
Từ (2) và (4) => ^KHI = ^DBC
=> tam giác HIK đồng dạng với tam giác BCD
thiếu câu d