mn cho em hỏi tứ giác có 2 góc =90 và hai cạnh bằng nhau có phải HCN ko ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
a.
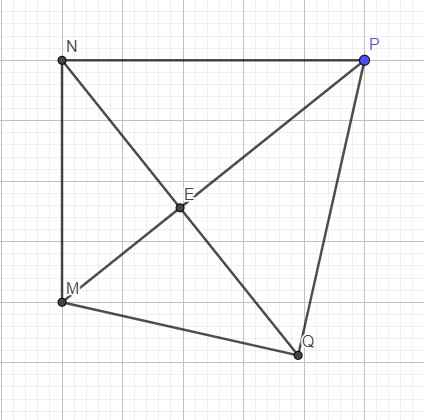
Xét hai tam giác MNP và MQP có:
\(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\\MP\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta MNP=\Delta MQP\left(c.c.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{NMP}=\widehat{QMP}\\\widehat{NPM}=\widehat{QPM}\end{matrix}\right.\) hay MP là phân giác của góc M và P
b.
Do \(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\end{matrix}\right.\) \(\Rightarrow MP\) là trung trực NQ
\(\Rightarrow MP\perp NQ\) (đpcm)
2 tháng 8 2021
Bài 2:
Nếu cả bốn góc trong một tứ giác đều là góc nhọn thì tổng của bốn góc đó sẽ nhỏ hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)
Nếu cả bốn góc trong một tứ giác đều là góc tù thì tổng của bốn góc đó sẽ lớn hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)
Ta có đpcm
2 tháng 8 2021
1) Xét ΔABC và ΔCDA có
AB=CD(gt)
\(\widehat{BAC}=\widehat{DCA}\)(hai góc so le trong, AB//CD)
AC chung
Do đó: ΔABC=ΔCDA(c-g-c)
Suy ra: \(\widehat{ACB}=\widehat{CAD}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC(Đpcm)
YT
24 tháng 7 2018
hinh vuong cx \(\Leftrightarrow\)tu giac deu ma bn
mik nghi nhu vay ak
12 tháng 12 2021
Theo 1 số trang mạng thì đó là 1 quy luật tự nhiên, luôn luôn đúng nhé
HT
2 tháng 8 2021
1) Xét ΔABC và ΔCDA có
AB=DC(gt)
\(\widehat{BAC}=\widehat{DCA}\)(hai góc so le trong, AB//CD)
AC chung
Do đó: ΔABC=ΔCDA(c-g-c)
Suy ra: \(\widehat{ACB}=\widehat{CAD}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC(Đpcm)
2 tháng 8 2021
Bài 2:
Nếu cả bốn góc đều là góc nhọn thì tổng bốn góc đó nhỏ hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)
Nếu cả bốn góc đều là góc tù thì tổng bốn góc đó lớn hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)
CM
9 tháng 3 2017
Chọn (A) có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
TH
3 tháng 3 2020
a, có số đo 4 góc của tứ giác ABCD lafn lượt tỉ lệ với 5, 8, 13, 10
\(\Rightarrow\frac{\widehat{A}}{5}=\frac{\widehat{B}}{8}=\frac{\widehat{C}}{13}=\frac{\widehat{D}}{10}\)
\(\Rightarrow\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{5+8+13+10}=\frac{\widehat{A}}{5}=\frac{\widehat{B}}{8}=\frac{\widehat{C}}{13}=\frac{\widehat{D}}{10}\) mà ^A + ^B + ^C + ^D = 360 do tứ giác ...
\(\Rightarrow\frac{360}{36}=10=\frac{\widehat{A}}{5}=\frac{\widehat{B}}{8}=\frac{\widehat{C}}{13}=\frac{\widehat{D}}{10}\)
\(\Rightarrow\widehat{A}=50;\widehat{B}=80;\widehat{C}=130;\widehat{D}=100\)
b, xét ΔABF có : ^ABF + ^BAF + AFB = 180 (định lí)
^ABF = 50 ; ^ABF = 80 (câu a)
=> ^AFB = 50
FM là phân giác của ^AFB
=> ^MFD = ^AFB : 2 (tính chất)
=> ^MFD = 50 : 2 = 25
^ADC + ^CDF = 180 (kề bù) mà ^ADC = 100 (câu a) => ^CDF = 80
ΔDMF có : ^MDA + ^DFM + ^DMF = 180 (định lí)
=> ^DMF = 75 (1)
ΔADE có : ^ADE + ^DAE + ^AED = 180 (Định lí)
^EAD = 50; ^ADE = 100
=> ^AED = 30 và (1)
ΔENM có : ^ENM + ^EMN + ^MNE = 180
=> ^ENM = 75 = ^EMN
=>ΔEMN cân tại E mà EO là pg của ^NEM (gt)
=> EO đồng thời là trung tuyến của ΔNEM (định lí)
=> O là trung điểm của MN (định nghĩa)
hình tự kẻ
chưa chắc nha bạn