Tìm GTLN và GTNN của \(M=3sinx+4cosx\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 9 2021
Sửa: \(y=3\sin x+4\cos x+2\)
Áp dụng BĐT Bunhiacopski được:
\(\left(3\sin x+4\cos x\right)^2\le\left(3^2+4^2\right)\left(\sin x^2+\cos x^2\right)=25\)
\(\Leftrightarrow-5\le3\sin x+4\cos x\le5\\ \Leftrightarrow-3\le3\sin x+4\cos x+2\le7\\ \Leftrightarrow y_{min}=-3\\ y_{max}=7\)
NM
2 tháng 11 2020
Xét phương trình: y=3sinx+4cosx+5
<=>3sinx+4cosx+5-y=0
Để phương trình có nghiệm:
=>32+42≥(5-y)2 (đẳng thức Bunhiacopxki)
<=>25≥25-10y+y2
<=>y2-10y≤0
<=>0≤y≤10
vậy miny=0; maxy=10
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 10 2020
1.
\(y=\frac{1}{2}sin2x-1\)
Do \(-1\le sin2x\le1\Rightarrow-\frac{3}{2}\le y\le-\frac{1}{2}\)
\(y_{min}=-\frac{3}{2}\) ; \(y_{max}=-\frac{1}{2}\)
2.
\(y=5+5\left(\frac{4}{5}cosx-\frac{3}{5}sinx\right)=5+5cos\left(x+a\right)\) với \(cosa=\frac{4}{5}\)
Do \(-1\le cos\left(x+a\right)\le1\Rightarrow0\le y\le10\)
\(y_{min}=0\) ; \(y_{max}=10\)
HK
5 tháng 8 2020
Cái đoạn theo điều kiện có nghiệm sao lại suy ra được thế kia hả anh?
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2020
Tồn tại x để \(a.sinx+b.cosx=c\) khi và chỉ khi \(a^2+b^2\ge c^2\)
NQ
1
8 tháng 8 2023
1: \(y=\sqrt{3}\cdot sin^2x-\left(1-sin^2x\right)+5\)
\(=sin^2x\left(\sqrt{3}+1\right)-1+5=sin^2x\left(\sqrt{3}+1\right)+4\)
\(0< =sin^2x< =1\)
=>\(0< =sin^2x\left(\sqrt{3}+1\right)< =\sqrt{3}+1\)
=>4<=y<=căn 3+5
y min=4 khi sin^2x=0
=>sin x=0
=>x=kpi
\(y_{max}=5+\sqrt{3}\) khi \(sin^2x=1\)
=>\(cos^2x=0\)
=>cosx=0
=>\(x=\dfrac{pi}{2}+kpi\)
2: \(y=5\left[\dfrac{3}{5}sinx+\dfrac{4}{5}cosx\right]+7\)
\(=5\cdot\left[sinx\cdot cosa+cosx\cdot sina\right]+7\)(Với cosa=3/5; sin a=4/5)
\(=5\cdot sin\left(x+a\right)+7\)
-1<=sin(x+a)<=1
=>-5<=5sin(x+a)<=5
=>-5+7<=y<=5+7
=>2<=y<=12
\(y_{min}=2\) khi sin (x+a)=-1
=>x+a=-pi/2+kp2i
=>\(x=-\dfrac{pi}{2}+k2pi-a\)
\(y_{max}=12\) khi sin(x+a)=1
=>x+a=pi/2+k2pi
=>\(x=\dfrac{pi}{2}+k2pi-a\)
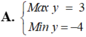
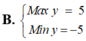
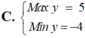
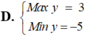
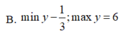
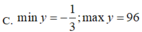
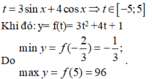
\(M^2=\left(3sinx+4cosx\right)^2\le\left(3^2+4^2\right)\left(sin^2x+cos^2x\right)=25\)
\(\Rightarrow-5\le M\le5\)
\(\Rightarrow M_{max}=5\) ; \(M_{min}=-5\)