3/2x4/3x5/4x...2022/2022
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=\dfrac{3}{2}x\dfrac{4}{3}x\dfrac{5}{4}x...x\dfrac{1999}{1998}x\dfrac{2000}{1999}=\dfrac{2000}{2}=1000\)

Lời giải:
\(A=\frac{3}{2}\times \frac{4}{3}\times \frac{5}{4}\times ....\times \frac{2000}{1999}\\
=\frac{3\times 4\times 5\times ....\times 2000}{2\times 3\times 4\times ...\times 1999}=\frac{2000}{2}=1000\)


vì \(\left(4x^2-4x+1\right)^{2022}\ge0\left(\forall x\right)\),\(\left(y^2-\dfrac{4}{5}y+\dfrac{4}{25}\right)^{2022}\ge0\left(\forall y\right)\),\(\left|x+y+z\right|\ge0\)
mà \(\left(4x^2-4x+1\right)^{2022}+\left(y^2+\dfrac{4}{5}y+\dfrac{4}{25}\right)^{2022}+\left|x+y-z\right|=0\)
=>\(\left\{{}\begin{matrix}4x^2-4x+1=0\\y^2+\dfrac{4}{5}y+\dfrac{4}{25}=0\\x+y-z=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-1=0\\y+\dfrac{2}{5}=0\\x+y-z=0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{-2}{5}\\\dfrac{1}{2}-\dfrac{2}{5}-z=0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{-2}{5}\\z=\dfrac{1}{10}\end{matrix}\right.\)
KL: vậy \(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{-2}{5}\\z=\dfrac{1}{10}\end{matrix}\right.\)

\(2022A=2022+2022^2+2022^3+2022^4+...+2022^{2018}\)
\(2021A=2022A-A=2022^{2018}-1\Rightarrow A=\dfrac{2022^{2018}-1}{2021}\)
\(\Rightarrow A< B\)

giúp tui với mai tui kt rùi
\(\dfrac{3}{2}\)x\(\dfrac{4}{3}\)x\(\dfrac{5}{4}\)x...x\(\dfrac{2022}{2023}\)
⇒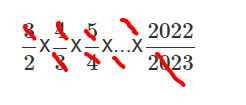
⇒\(\dfrac{2022}{2}\)=1011