Câu 1:Một thùng hàng có khối lượng 100 kg đang nằm yên trên nền nhà. Một lực kéo F có phương nằm ngang tác dụng vào thủng hàng. Sau khi tác dụng được 5 s thì thùng hàng đạt vận tốc 10 m/s. Biết nợ số ru sát trượt giữa thùng hàng và nền nhà là 0,25. Lấy g = 9,8 m/s. a) Tính gia tốc của thùng hàng khi chuyển động. b) Vẽ các lực tác dụng vào thùng hàng trong quá trình chuyển động. Nêu tên của các lực đó. c) Tính độ lớn của lực ma sát trượt tác dụng vào thùng hàng. d) Tính độ lớn của lực kéo.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gia tốc vật:
\(v=v_0+at\Rightarrow a=\dfrac{v-v_0}{t}=\dfrac{5-0}{10}=0,5\)m/s2
Định luật ll Niu-tơn ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)\(\Rightarrow7-\mu mg=m\cdot a\)
Hệ số ma sát trượt:
\(\Rightarrow\mu=\dfrac{7-m\cdot a}{mg}=\dfrac{7-2\cdot0,5}{2\cdot10}=0,3\)

Chọn đáp án B
? Lời giải:
Từ khi bắt đầu chuyển động đến khi dừng hẳn vật chuyển động trong hai giai đoạn.
• Giai đoạn I: Trong 10 giây đầu tiên vật chuyển động với gia tốc a1 (v0 = 0):
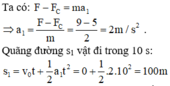
• Giai đoạn II: Vật động chậm dần đều với gia tốc a2 khi F = 0.
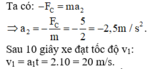
Quãng đường s2 xe chuyến động chậm dần đều với gia tốc a2 từ tốc độ v1 đến khi dừng hẳn (v2 = 0):
s 2 = v 2 2 − v 1 2 2 a 2 = 0 − 20 2 2. − 2 , 5 = 80 m
Vậy quãng đường xe đi được từ lúc bắt đầu chuyển động đến khi dừng hẳn là:
s = s 1 + s 2 = 180 m

a)\(v=54km/h=15m/s\)
Gia tốc của vật: \(v^2-v_0^2=2aS\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2S}=\dfrac{15^2-0^2}{2\cdot112,5}=1m/s^2\)
b)Theo định luật ll Niuton: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\Rightarrow F_{ms}=F-m.a=12-3\cdot1=9N\)
Hệ số ma sát: \(F_{ms}=\mu mg\)
\(\Rightarrow\mu=\dfrac{F_{ms}}{m\cdot g}=\dfrac{9}{3\cdot10}=0,3\)

a)Độ lớn lực ma sát:
\(F_{ms}=\mu mg=0,02\cdot10\cdot10=2N\)
Công lực ma sát: \(A_{ms}=F_{ms}\cdot s=2\cdot5=10m\)
b)Bảo toàn động năng:
\(A_F=\Delta W=\dfrac{1}{2}m\left(v_2^2-v_1^2\right)=\dfrac{1}{2}\cdot10\cdot\left(5^2-0^2\right)=125J\)
\(\Rightarrow F_k=\dfrac{A_F}{s}=\dfrac{125}{5}=25N\)

a) gia tốc của vật a = V - Vo / t = 2 - 0 / 2 = 1 m/s2
Quảng đường vật đi được V2 - Vo 2 =2 aS
<=> 22 - 02 = 2.1.s => s= 2m
b) Ta có P = N= mg= 0,7.10 = 7 N ( do vật nằm trên mặt phảng ngang và có F // mp )
Fmst =u.N=0.3.7= 2.1 N
ta lại có a = F-Fmst /m
<=> 1=F - 2.1 /0.3 => F = 2.4 N

Áp dụng định luật II-Niuton ta có: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{F_{ms}}+\overrightarrow{N}=m\overrightarrow{a}\)
Chiếu vector lực theo phương ngang và phương thẳng đứng ta được
\(\left\{{}\begin{matrix}F-F_{ms}=ma\\P=N\end{matrix}\right.\)
\(\Rightarrow F-N\mu=ma\)
\(\Leftrightarrow F-mg\mu=ma\Leftrightarrow15-5.0,1.10=5a\Rightarrow a=2\) m/s2
Vận tốc của vật sau 3s là: \(v=v_0+at=0+2.3=6\) m/s
Một lò xo có khối lượng không đáng kể, một đầu được gắn cố định, đầu kia treo vật nặng có khối lượng m = 300 g, ở vị trí cân bằng lò xo dãn ra 6 cm. Lấy g = 10 m/s2
a. Tính độ cứng của lò xo.
b. Nếu treo thêm vật m’= 200 g vào đầu lò xo trên thì độ dãn của lò xo lúc ấy là bao nhiêu ?