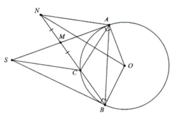
Bài IV (3,0 điểm) Cho đường tròn (O,R) và một điểm S nằm ngoài đường tròn. Từ điểm S vẽ hai tiếp tuyến SA, SB với (O) (A, B là các tiếp điểm).
1) Chứng minh tứ giác OASB là tứ giác nội tiếp.
2) Kẻ đường kính BD của đường tròn (O). Đường thẳng SD cắt đường tròn (O) tại điểm C (C khác D ). Chứng minh rằng SA.SB = SC.SD.
3) Gọi I là giao điểm của hai đoạn thẳng SO và AB . Tia CI cắt...
Đọc tiếp
Bài IV (3,0 điểm) Cho đường tròn (O,R) và một điểm S nằm ngoài đường tròn. Từ điểm S vẽ hai tiếp tuyến SA, SB với (O) (A, B là các tiếp điểm). 1) Chứng minh tứ giác OASB là tứ giác nội tiếp. 2) Kẻ đường kính BD của đường tròn (O). Đường thẳng SD cắt đường tròn (O) tại điểm C (C khác D ). Chứng minh rằng SA.SB = SC.SD. 3) Gọi I là giao điểm của hai đoạn thẳng SO và AB . Tia CI cắt đường tròn (O) tại điểm thứ hai là M . Chứng minh tam giác SCI đồng dạng với tam giác SOD và ba điểm A, O, M là ba điểm thẳng hàng.
1: góc OAS+góc OBS=90+90=180 độ
=>OASB nội tiép
2: Xét ΔSAC và ΔSDA có
góc SAC=góc SDA
góc ASC chung
=>ΔSAC đồng dạng với ΔSDA
=>SA/SD=SC/SA
=>SA^2=SD*SC=SA*SB
3: Xét (O) có
SA,SB là tiêp tuyến
=>SA=SB
mà OA=OB
nên OS là trung trực của AB
=>OS vuông góc AB tại I
=>SI*SO=SA^2=SC*SD
=>SI/SD=SC/SO
=>ΔSIC đồng dạng với ΔSDO