cho hai số x,y thỏa mãn điều kiện 3x+y=1
tìm giá trị nhỏ nhất của biểu thức A=3x2+y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 11 2019
Đáp án B
Ta có:
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
Xét hàm số f t = 3 t . log 2 t trên khoảng 0 ; + ∞ , có f ' t = 3 t ln 3. log 2 t + 3 t t . ln 2 > 0 ; ∀ t > 0
Suy ra f t là hàm số đồng biến trên 0 ; + ∞ mà
f x − y 2 = f 2 − 2 x y ⇒ x 2 + y 2 = 2
Khi đó:
M = 2 x 3 + y 3 − 3 x y = 2 x + y x + y 2 − 3 x y − 3 x y ⇔ 2 M = 2 x + y 2 x + y 2 − 3.2 x y − 3.2 x y 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6 = 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
Với a = x + y ∈ 0 ; 4
Xét hàm số f a = − 2 a 3 − 3 a 2 + 12 a + 6 trên 0 ; 4 ,
suy ra m ax 0 ; 4 f a = 13.
Vậy giá trị lớn nhất của biểu thức M là 13 2
CM
10 tháng 6 2017
Đáp án B
Ta có
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
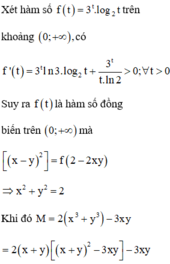
⇔ 2 M = 2 x + y 2 x + y 2 − 3.2. x y − 3.2 x y = 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6
= 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
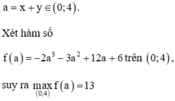
Vậy giá trị lớn nhất của biểu thức M là 13 2
CM
9 tháng 7 2017
Đáp án C.
Từ giả thiết ta có
ln x + y + 1 + 3 x + y + 1 = ln 3 x y + 3.3 x y (*)
Xét f t = ln t + 3 t hàm trên 0 ; + ∞ , ta có f ' t = 1 t + 3 > , ∀ t > 0
Do đó * ⇔ x + y + 1 = 3 x y ⇔ 3 x y − 1 = x + y ≥ 2 x y ⇔ 3 xy − 2 x y − 1 ≥ 0
Suy ra x y ≥ 1 ⇒ x y ≥ 1.
27 tháng 12 2018
Ta có: 3x + y = 1 => y = 1 - 3x
=> M = 3x2 + y2 = 3x2 + (1-3x)2
= 3x2 + 1 - 6x + 9x2
= 12x2 - 6x + 1
= 12.(x2 -\(\frac{1}{2}x\) + \(\frac{1}{12}\))
= 12.((x2 - 2. \(\frac{1}{4}x\)+ \(\frac{1}{16}\)) - \(\frac{1}{16}\)+ \(\frac{1}{12}\))
= 12.((x-\(\frac{1}{4}\))2 + \(\frac{1}{48}\))
= 12. (x-\(\frac{1}{4}\))2 + \(\frac{1}{4}\)
=> M \(\ge\)\(\frac{1}{4}\)
Dấu ''='' xảy ra khi: (x - \(\frac{1}{4}\))2 = 0 => x = \(\frac{1}{4}\)
Vậy Mmin= \(\frac{1}{4}\)khi x= \(\frac{1}{4}\)
CM
6 tháng 11 2017
Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
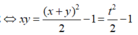
Từ 
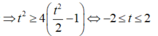
P = f(t)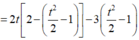 
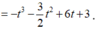
Xét f(t) trên [-2;2].
Ta có 
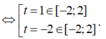
Bảng biến thiên
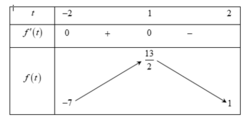
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có 
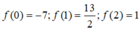
Suy ra kết luận.