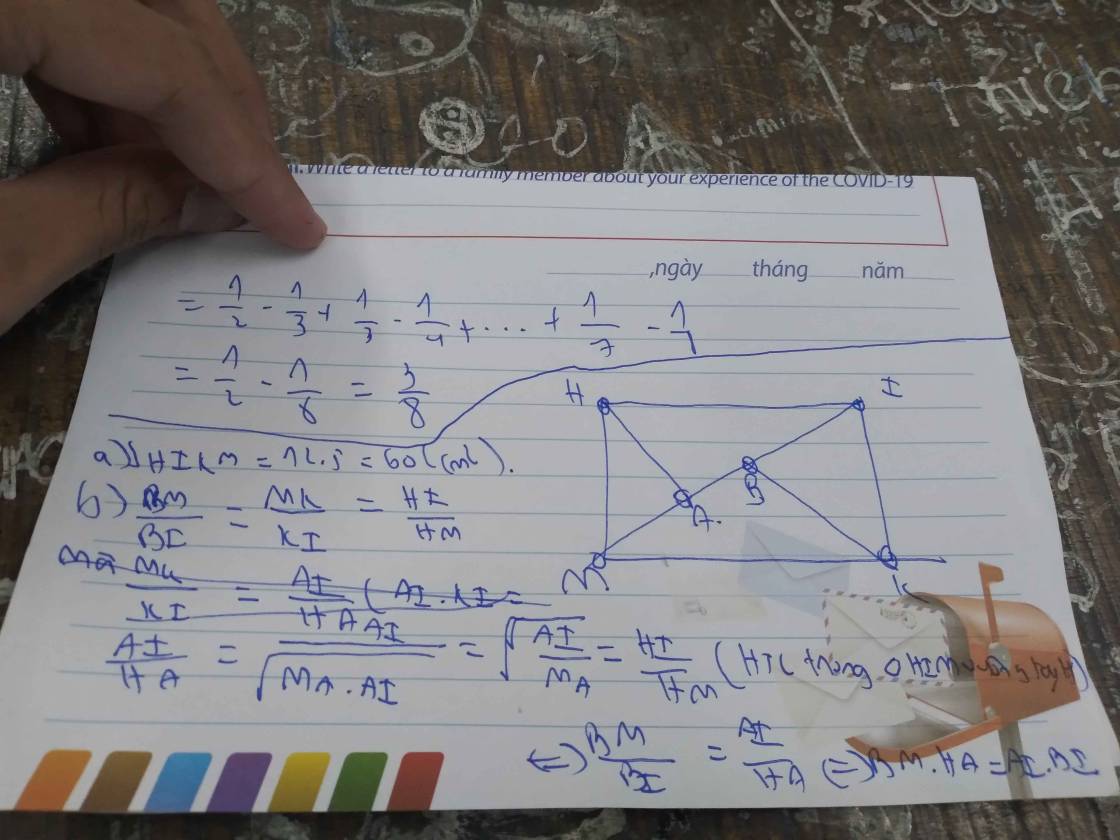
Cho hình chữ nhật HIKM có HI = a = 12cm, MQ = b = 5cm. Gọi A là giác đường vuông góc hạ từ H xuống IM. Phân giác của góc IKM cắt IM tại B.
a Tính diện tích hình chữ nhật HIKM?
b Chứng minh rằng: HA.BM = AI.BI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHAD vuông tại H và ΔABD vuông tại A có
góc ADB chung
=>ΔHAD đồng dạng với ΔABD
b: ΔHAD đồng dạng vơi ΔABD
=>DH/DA=DA/DB
=>DA^2=DH*DB

a: Áp dụng định lí Pytago vào ΔBDC vuông tại C, ta được:
\(DB^2=BC^2+CD^2\)
\(\Leftrightarrow DB^2=12^2+9^2=225\)
hay DB=15(cm)
Xét ΔBDC có
BE là đường phân giác ứng với cạnh DC
nên \(\dfrac{EC}{ED}=\dfrac{BC}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)
b: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD

Vì
△
AHB đồng dạng
△
BCD với tỉ số đồng dạng: 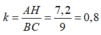
Ta có:  =
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
=
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
S B C D = 1/2 BC.CD = 1/2 .12.9 = 54( c m 2 )
Vậy S A H B = 0 , 64 . S B C D = 0,64.54 = 34,56 ( c m 2 ).

a) Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//DC)
Do đó: ΔAHB\(\sim\)ΔBCD(g-g)
b) Xét ΔBCD có CE là đường phân giác ứng với cạnh BD(gt)
nên \(\dfrac{EB}{ED}=\dfrac{BC}{CD}\)(Tính chất đường phân giác của tam giác)(1)
Ta có: ΔAHB\(\sim\)ΔBCD(cmt)
nên \(\dfrac{AH}{BC}=\dfrac{HB}{CD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AH}{HB}=\dfrac{BC}{CD}\)(2)
Từ (1) và (2) suy ra \(\dfrac{AH}{HB}=\dfrac{EB}{ED}\)
hay \(AH\cdot ED=HB\cdot EB\)(đpcm)

a) Xét tứ giác AMIN có :
\(MI//AN\left(\perp AM\right)\)
\(MA//IN\left(\perp AN\right)\)
\(\Rightarrow\)Tứ giác AMIN là hình bình hành
mà \(\widehat{A}=90^o\)
\(\Rightarrow\)Tứ giác AMIN là hình chữ nhật
b) Ta có : AM // NI (cmt)
\(\Rightarrow MB//NI\left(1\right)\)
Xét \(\Delta ACB\)có :
BI = IC (gt)
AM // NI (cmt)
\(\Rightarrow\)NI là đường trunbg bình của \(\Delta ACB\)
\(\Rightarrow NI=\frac{1}{2}AB\left(2\right)\)
mà tứ giác AMIN là hình chữ nhật
\(\Rightarrow AM=NI\left(3\right)\)
Từ (2) và (3) \(\Rightarrow AM=\frac{1}{2}AB\)
\(\Rightarrow\)M là trung diểm của AB
\(\Rightarrow AM=MB\left(4\right)\)
Từ (2) và (4) \(\Rightarrow BM=NI\left(5\right)\)
Từ (1) và (5) \(\Rightarrow\)tứ giác NMBI là hình bình hành
c) Xét \(\Delta ABC\)có :
BI = IC (gt)
BM = MA (cmt)
\(\Rightarrow\)MI là dường trung bình của \(\Delta ABC\)
\(\Rightarrow MI=\frac{1}{2}AC\left(6\right)\)
Ta có : NI là đường trung binh của \(\Delta ACB\)(cmt)
\(\Rightarrow AN=NC\)
\(\Rightarrow NC=\frac{1}{2}AC\left(7\right)\)
Từ (6) và (7) \(\Rightarrow MI=NC=5\left(cm\right)\)
Vậy NC = 5cm

a) Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH = góc BDC(hai góc so le trong, AB//DC)
góc BCD = góc AHB(hai góc vuông)
Do đó: ΔAHB∼ΔBCD(g-g)
b) Xét ΔBCD có CE là đường phân giác ứng với cạnh BD(gt)
nên \(\dfrac{EB}{ED}\)=\(\dfrac{BC}{CD}\)(Tính chất đường phân giác của tam giác)(1)
Ta có: ΔAHB∼∼ΔBCD(cmt)
nên\(\dfrac{AH}{BC}\)=\(\dfrac{HB}{CD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay\(\dfrac{AH}{BH}\)=\(\dfrac{BC}{CD}\)(2)
Từ (1) và (2) suy ra \(\dfrac{AH}{BH}\)=\(\dfrac{EB}{ED}\)
hay AH⋅ED=HB⋅EB(đpcm)

Phần a,b nha
a)Xét tứ giác MDHE, có:
MDHˆ=900MDH^=900
Mˆ=900M^=900
HEMˆ=900HEM^=900
=> Tứ giác MDHE là hình chữ nhật
b) Gọi giao điểm của MH là DE là O MDHE là hình chữ nhật nên hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
=> OH=OE
Xét tam giác EOH, có:
OH=OE(CMT)
=> Tam giác EOH cân tại O
=> H1ˆ=E1ˆH1^=E1^
Xét DEHP vuông tại E ,có:
A là trung điểm PH
=> AE = AH.
=> H2ˆ=E2ˆH2^=E2^
=> AEOˆ=AHOˆAEO^=AHO^ =900=900
Từ đó góc AEO = 900
hay tam giác DEA vuông tại E.

a)
vì ABCD hình chữ nhật nên ta có AB//CD
=> góc ABH= góc BDC ( so le trong, AB//CD)
xét tam giác AHB,BCD có
góc A= góc C =90
góc ABH=BDC(cmt)
=> tam giác AHB đồng dạng với tam giác CDB (gg)
b)
vì ABCD hcn nên
AB=CD=12
BC=AD=9
AD Đlí pytado cho tam giác vuông CDB có
BD2=BC2+DC2
BD2=81+144
BD=15cm
theo câu a) ta có
AH/AB=BC/BD
=> AH= AB.BC chia BD
AH= 12.9 chia 15
AH= 7.2CM
C)
BD