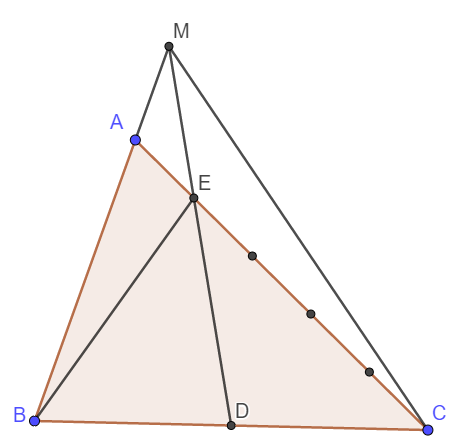
Cho tam giác ABC. Gọi D là điểm chính giữa đoạn BC. Lấy điểm E trên cạnhAC sao cho AE =1/5 AC. Nối DE kéo dài cắt đường thẳng AB tại M, nối M với C. Biết diện tích tam giác AME=20 cm2. Hãy tính
A, diện tích tam giác MEC
B, diện tích tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)

Cho tam giác ABC. Gọi D là điểm chính giữa của cạnh BC. Lấy E trên cạnh AC sao cho AE bằng 1/5 AC. Nối D với E. Kéo dài DE cắt AB kéo dài tại M. Nối M với C. Biết diện tích AME bằng 20 cm2 .Tính diện tích MEC và ABC?
Được cập nhật 22 tháng 5 2019 lúc 20:10
4
![]()
![]()
Hoàng Thị Thu Huyền Quản lý
7 tháng 3 2018 lúc 10:05

a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên SMEC=4SMAE=4×20=80(cm2)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên SMBD=SMCD
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên SEBD=SECD
Vậy nên SMBE=SMEC=80(cm2)

Kẻ MK vuông góc AC
\(S_{AME}=\dfrac{1}{2}\cdot MK\cdot AE\)
\(S_{MEC}=\dfrac{1}{2}\cdot MK\cdot EC\)
mà AE=1/4*EC
nên \(S_{AME}=\dfrac{1}{4}\cdot S_{MEC}\)
=>\(S_{MEC}=80\left(cm^2\right)\)

D là điểm chính giữa của đoạn thẳng BC
=>D là trung điểm của BC
=>BD/BC=1/2
=>\(S_{ABD}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot360=180\left(cm^2\right)\)
AE=ED
A,E,D thẳng hàng
Do đó; E là trung điểm của AD
=>\(AE=\dfrac{1}{2}AD\)
=>\(S_{ABE}=\dfrac{1}{2}\cdot S_{ABD}=\dfrac{1}{2}\cdot180=90\left(cm^2\right)\)

tick cho mình đi
Lời giải
a) Tính diện tích tam giác ABC
Vì MA = 3/2 MC, nên MC = 2MA/3.
Vì CE = 1/2 BC, nên BC = 2CE.
Vì D là giao của BM và AE, nên MD = MC - ME = 2MA/3 - MC/2 = MA/6.
Vì AM = 45cm, nên MC = 2AM/3 = 30cm, BC = 60cm và MD = AM/6 = 7.5cm.
Diện tích tam giác ABC là:
b) So sánh diện tích tam giác ABM và diện tích tam giác CME
Vì AM = 3/2 MC, nên BM = 2MC/3.
Vì ME = MC/2, nên BM = 4ME/3.
Vì BM/ME = 4/3, nên diện tích tam giác ABM/diện tích tam giác CME = 4/3.
Vậy, diện tích tam giác ABM lớn hơn diện tích tam giác CME.
c) So sánh diện tích tam giác MED và diện tích tam giác MAD
Vì MD = AM/6, nên diện tích tam giác MED/diện tích tam giác MAD = AM/6 * 1/AM = 1/6.
Vậy, diện tích tam giác MED nhỏ hơn diện tích tam giác MAD.
Vẽ hình
[Hình tam giác ABC]
Trong hình trên, ta có:
Kết luận