Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Kẻ MK vuông góc AC
\(S_{AME}=\dfrac{1}{2}\cdot MK\cdot AE\)
\(S_{MEC}=\dfrac{1}{2}\cdot MK\cdot EC\)
mà AE=1/4*EC
nên \(S_{AME}=\dfrac{1}{4}\cdot S_{MEC}\)
=>\(S_{MEC}=80\left(cm^2\right)\)
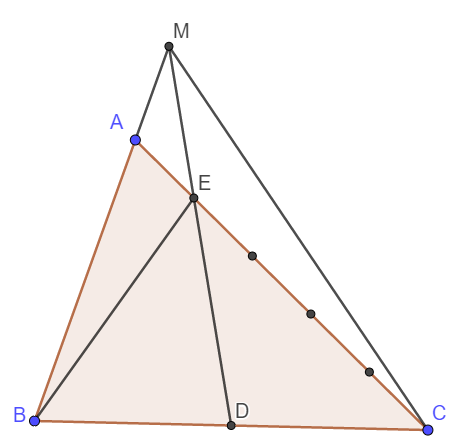
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)
Cho tam giác ABC. Gọi D là điểm chính giữa của cạnh BC. Lấy E trên cạnh AC sao cho AE bằng 1/5 AC. Nối D với E. Kéo dài DE cắt AB kéo dài tại M. Nối M với C. Biết diện tích AME bằng 20 cm2 .Tính diện tích MEC và ABC?
Được cập nhật 22 tháng 5 2019 lúc 20:10
4
Hoàng Thị Thu Huyền Quản lý
7 tháng 3 2018 lúc 10:05
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên SMEC=4SMAE=4×20=80(cm2)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên SMBD=SMCD
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên SEBD=SECD
Vậy nên SMBE=SMEC=80(cm2)
D là điểm chính giữa của đoạn thẳng BC
=>D là trung điểm của BC
=>BD/BC=1/2
=>\(S_{ABD}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot360=180\left(cm^2\right)\)
AE=ED
A,E,D thẳng hàng
Do đó; E là trung điểm của AD
=>\(AE=\dfrac{1}{2}AD\)
=>\(S_{ABE}=\dfrac{1}{2}\cdot S_{ABD}=\dfrac{1}{2}\cdot180=90\left(cm^2\right)\)