Giúp mình với. Mình đang cần gấp ạ😓😓😓

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A. MgSO4
- Liên kết ion được hình thành bởi cation kim loại Mg2+ và anion gốc axit SO42-
- Liên kết cộng hóa trị giữa S và O.
A: MgSO4
Liên kết ion giữa Mg2+ và SO42-, liên kết cộng hóa trị giữa S và O

Bài 1:
Ta có số tiền tủ lạnh sau khi giảm lần 1 là: \(15000000-15000000.20\%=12000000đ\)
Số tiền tủ lạnh sau khi giảm lần 2 là: \(12000000-12000000.5\%=11400000đ\)
Số tiền cửa hàng thu được sau khi bán 5 cái tủ lạnh: \(11400000.5=57000000đ\)




ta có:
\(\dfrac{P_1}{P}=\dfrac{S_1}{S}=\dfrac{\pi R^2}{\dfrac{4}{\pi R^2}}=\dfrac{1}{4}\)
\(\dfrac{P_2}{P}=\dfrac{S-2S_1}{S}=\dfrac{S-\dfrac{S}{2}}{S}=\dfrac{1}{2}\)
<=>\(\dfrac{P_1}{P_2}=\dfrac{1}{\dfrac{4}{\dfrac{1}{2}}}=\dfrac{1}{2}\)
ta tiếp có hệ pt:
\(\left\{{}\begin{matrix}\dfrac{OO_2}{OO_1}=\dfrac{P_1}{P_2}=\dfrac{1}{2}\\OO_2+OO_1=\dfrac{R}{2}\end{matrix}\right.\)
ra được :
\(OO_1=\dfrac{R}{3}\) và \(OO_2=\dfrac{R}{6}\)

\(1,=20x^2-15x+10x-20x^2=-5x\\ 2,=4x^2-20x+25-4x^2+18x-18=7-2x\\ 3,=\left(6x^3-4x^2-12x+8x+15x-10\right):\left(3x-2\right)\\ =\left(3x-2\right)\left(2x^2-4x+5\right):\left(3x-2\right)\\ =2x^2-4x+5\\ 4,=\dfrac{5x+25-2x+10+x^2+2x-35}{\left(x+5\right)\left(x-5\right)}=\dfrac{x\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}=\dfrac{x}{x-5}\\ 5,=\dfrac{3x-8-x-6}{x-7}+\dfrac{\left(x-2\right)\left(x+2\right)}{x-2}=\dfrac{2\left(x-7\right)}{x-7}+x+2=2+x+2=x+4\\ 6,=\dfrac{x^2+8x+16+2x-8-6x-8}{\left(x-4\right)\left(x+4\right)}=\dfrac{x\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{x}{x-4}\\ 7,=\dfrac{x\left(x-7\right)}{2x\left(x+3\right)}\cdot\dfrac{4\left(x-3\right)\left(x+3\right)}{\left(x-7\right)^2}=\dfrac{2\left(x-3\right)}{x-7}\)

a: Xét tứ giác AHCE có
M là trung điểm của AC
M là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật

a)Trạng thái ban đầu: \(\left\{{}\begin{matrix}p_1=20Pa\\V_1=100cm^3=0,1l\end{matrix}\right.\)
Trạng thái sau: \(\left\{{}\begin{matrix}p_2=10Pa\\V_2=???\end{matrix}\right.\)
Áp dụng quá trình đẳng nhiệt ta có:
\(p_1V_1=p_2V_2\Rightarrow20\cdot0,1=10\cdot V_2\)
\(\Rightarrow V_2=0,2l=200cm^3\)
b)Trạng thái đầu: \(\left\{{}\begin{matrix}p_1=20Pa\\T_1\end{matrix}\right.\)
Trạng thái sau: \(\left\{{}\begin{matrix}p_2=???\\T_2=3T_1\end{matrix}\right.\)
Áp dụng quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{20}{T_1}=\dfrac{p_2}{3T_1}\Rightarrow p_2=60Pa\)
 Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé  Giúp mình với ạ, mình đang cần gấp ạ
Giúp mình với ạ, mình đang cần gấp ạ


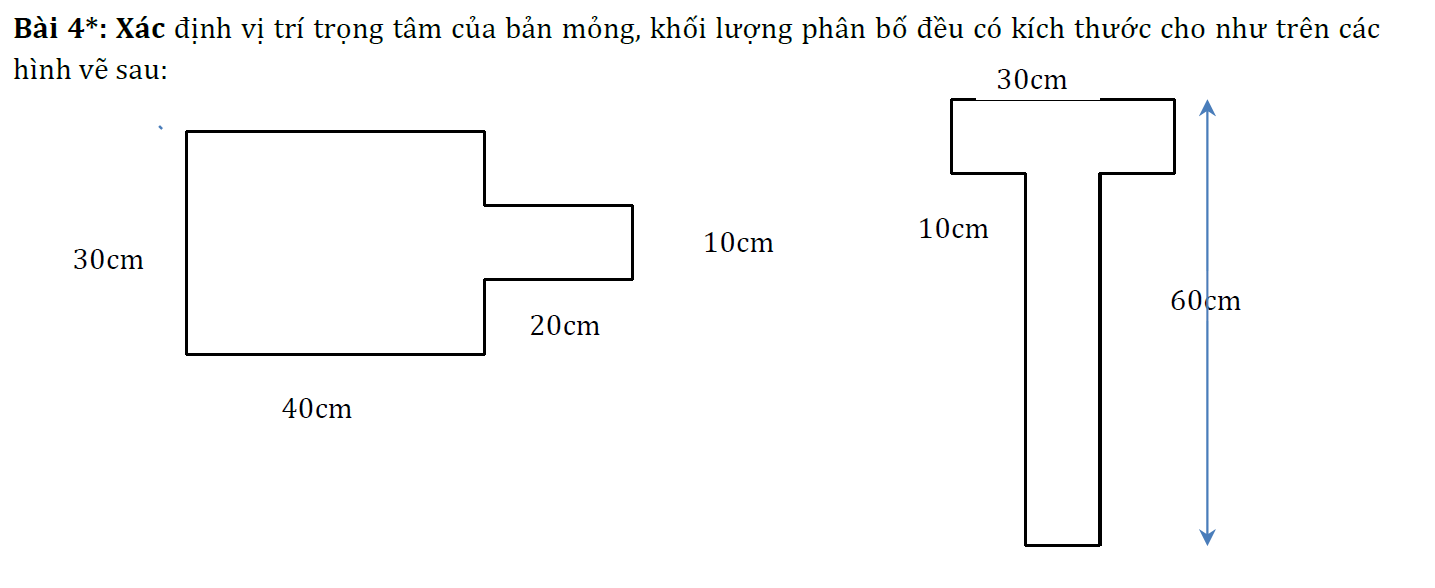




27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)