Cho tam giác ABC nội tiếp đường tròn (O). Phân giác trong của góc BAC cắt BC tại D và cắt đường tròn tại M. Phân giác ngoài tại A cắt đường thẳng BC tại E và cắt đường tròn tại N. Gọi K là trung điểm của DE. Chứng minh
a) MN vuông góc với BC tại trung điểm của BC
b) Góc ABN = EAK

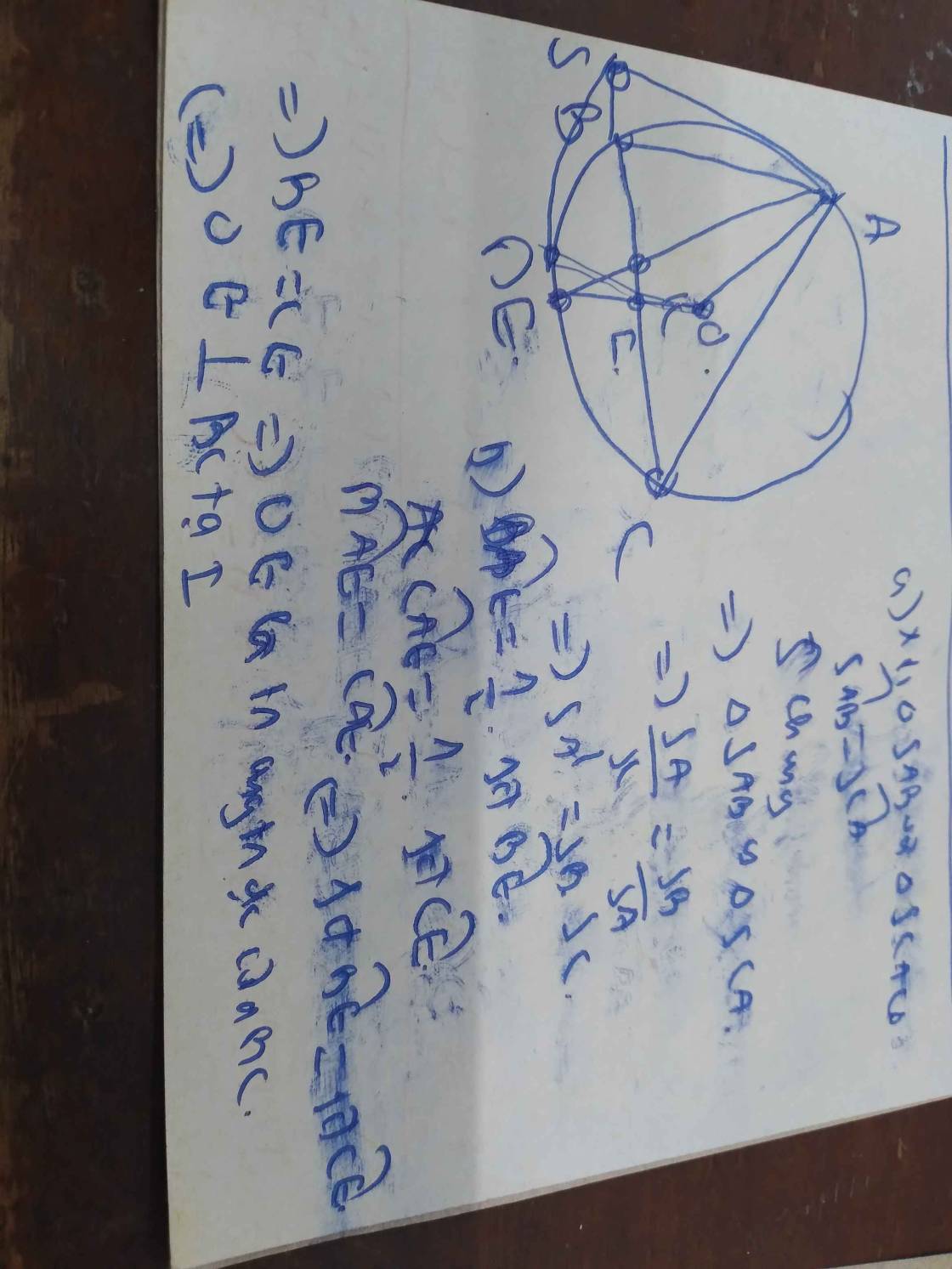
a. Do AN và AM là hai tia phân giác nên \(AN⊥AM\). Vậy thì MN là đường kính của đường tròn O.
Theo tính chất đường kính dây cung, MN vuông góc với BC tại trung điểm BC.
b. Do tam giác AED vuông tại A, K là trung điểm DE nên \(\widehat{EAK}=\widehat{AEK}=\frac{sđ\widebat{NC}-sđ\widebat{AB}}{2}\)(Góc có đỉnh bên ngoài đường tròn)
Lại có MN là đường kính nên \(sđ\widebat{NB}+sđ\widebat{BM}=sđ\widebat{NC}+sđ\widebat{CM}\);
Lại do AM là phân giác nên \(\widehat{BAM}=\widehat{CAM}\Rightarrow sđ\widebat{BM}=sđ\widebat{CM}\) (Góc nội tiếp)
Vậy thì \(sđ\widebat{NB}=sđ\widebat{NC}\)
Khi đó \(\widehat{EAK}=\widehat{AEK}=\frac{sđ\widebat{NC}-sđ\widebat{AB}}{2}=\frac{sđ\widebat{NB}-sđ\widebat{AB}}{2}=\frac{sđ\widebat{AN}}{2}=\widehat{ABN}\) (góc nội tiếp).