Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Kẻ Ax là tiếp tuyến của đường tròn (O)
=> Ax ⊥ AO tại A (1)
Ta có : \(\widehat{xAB} = \widehat{ABC} \) ( góc tạo bởi tiếp tuyến và dây và góc nội tiếp chắn \(\widehat{AC}\) )
Lại có : \(\begin{cases} \widehat{ABC} + \widehat{ACB} + \widehat{BAC} = 180^o\\ \widehat{ADQ} + \widehat{AQD} + \widehat{BAC} = 180^o \end{cases} \)
Mà \(\widehat{AQD} = \widehat{ACB}\) ( 2 góc nội tiếp cùng chắn cung \(\widehat{BD} \) )
=> \(\widehat{ABC} = \widehat{ADB} \) => Ax // QD (2)
Từ (1) và (2) => QD ⊥ AO


Gọi K đối xứng với F qua M.
Tứ giác FBKC là hình bình hành\(\Rightarrow FC//BK\)
\(\Rightarrow\widehat{BKM}=\widehat{MEB};\widehat{BKM}=\widehat{MFA}\).Mà \(\widehat{AEM}=\widehat{MFA}\Rightarrow\widehat{BKM}=\widehat{MEB}\Rightarrow\)Tứ giác BMKE nội tiếp
\(\Rightarrow\widehat{BEK}=\widehat{DAE};\widehat{BEK}=\widehat{FMD}=\widehat{FAD}=\widehat{DAE}\)
\(\Rightarrow\widehat{BEK}=\widehat{DAE}\Rightarrow AD//EK\)
Do N là trung điểm của EF, M là trung điểm của FK \(\Rightarrow MN//EK\)
\(\Rightarrow MN//AD\left(đpcm\right)\)
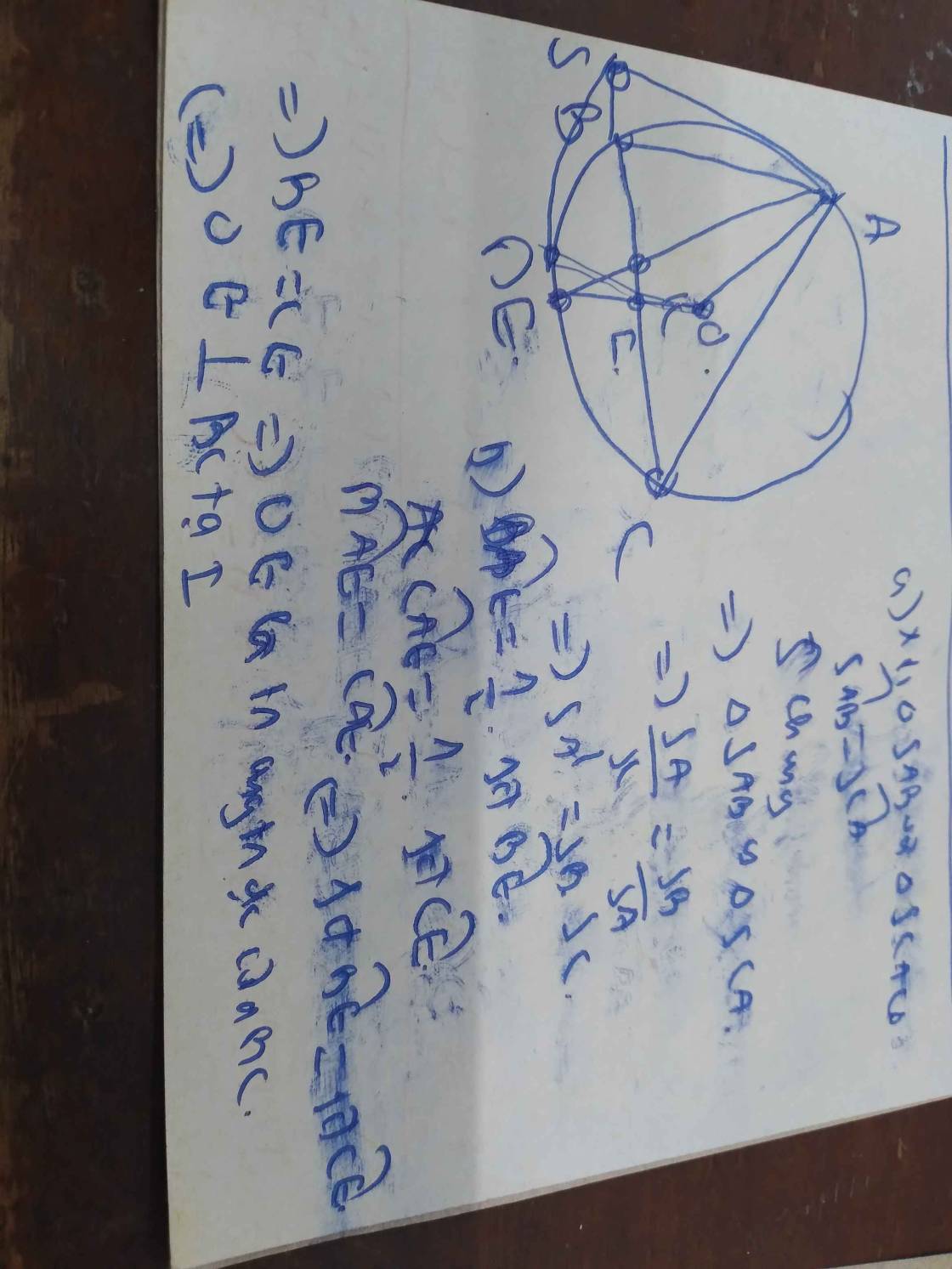
a. Do AN và AM là hai tia phân giác nên \(AN⊥AM\). Vậy thì MN là đường kính của đường tròn O.
Theo tính chất đường kính dây cung, MN vuông góc với BC tại trung điểm BC.
b. Do tam giác AED vuông tại A, K là trung điểm DE nên \(\widehat{EAK}=\widehat{AEK}=\frac{sđ\widebat{NC}-sđ\widebat{AB}}{2}\)(Góc có đỉnh bên ngoài đường tròn)
Lại có MN là đường kính nên \(sđ\widebat{NB}+sđ\widebat{BM}=sđ\widebat{NC}+sđ\widebat{CM}\);
Lại do AM là phân giác nên \(\widehat{BAM}=\widehat{CAM}\Rightarrow sđ\widebat{BM}=sđ\widebat{CM}\) (Góc nội tiếp)
Vậy thì \(sđ\widebat{NB}=sđ\widebat{NC}\)
Khi đó \(\widehat{EAK}=\widehat{AEK}=\frac{sđ\widebat{NC}-sđ\widebat{AB}}{2}=\frac{sđ\widebat{NB}-sđ\widebat{AB}}{2}=\frac{sđ\widebat{AN}}{2}=\widehat{ABN}\) (góc nội tiếp).