bài này em ko hiểu có thể giải giúp em đc ko ạ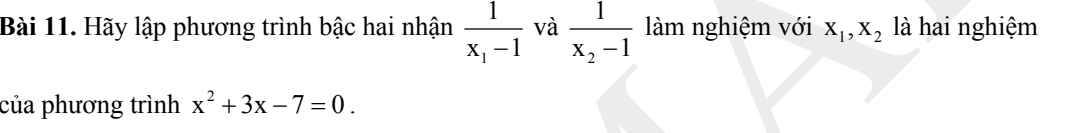
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Để phấn số đó bé hơn 1 và có tử số lớn nhấ có thể thì tử số= 2015-1=2014
=> phấn số đó là: 2014/2015
Để phấn-> phân số đó bé hơn 1 và có tử số lớn nhấ có thể thì tử số= 2015-1=2014
=> phấn-> phân số đó là: 2014/2015


Gọi số sách là x
Theo đề, ta có: \(x+2\in BC\left(10;25\right)\)
\(\Leftrightarrow x+2\in B\left(50\right)\)
mà x là số lớn nhất có 3 chữ số và thỏa mãn đề bài
nên x+2=1000
hay x=998

\(g'\left(x\right)=3.f'\left(3x\right)+9=0\Rightarrow f'\left(3x\right)=-3\Rightarrow\left[{}\begin{matrix}3x=-1\\3x=0\\3x=1\\3x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=0\\x=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\) Trên \(\left[-\dfrac{1}{3};\dfrac{1}{3}\right]\) hàm \(g\left(x\right)\) đạt cực đại tại \(x=0\) và cực tiểu tại \(x=-\dfrac{1}{3};\dfrac{1}{3}\)
\(\Rightarrow g\left(x\right)_{max}=g\left(0\right)=f\left(0\right)\)


10: =>1/2x=3/4 và x+y=2
=>x=3/4*2=3/2 và y=1/2
11:=>4x+5y=3 và 4x-12y=20
=>17y=-17 và x-3y=5
=>y=-1 và x=3y+5=-3+5=2
12: =>7x-2y=1 và 6x+2y=12
=>13x=13 và 3x+y=6
=>x=1 và y=3
13:=>2/x=1 và 1/x-1/y=1/5
=>x=2 và 1/y=1/2-1/5=3/10
=>y=10/3 và x=2
14: =>12/x-16/y=8 và 12/x-15/y=9
=>-1/y=-1 và 4/x-5/y=3
=>y=1 và 4/x=3+5=8
=>x=1/2 và y=1

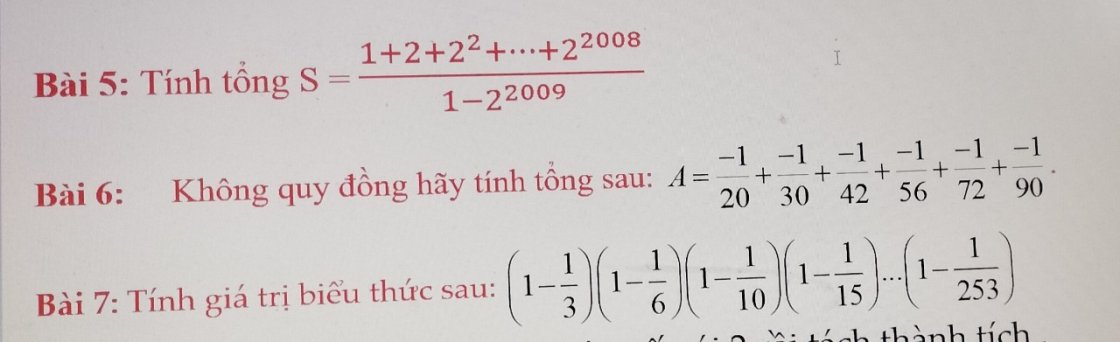 các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
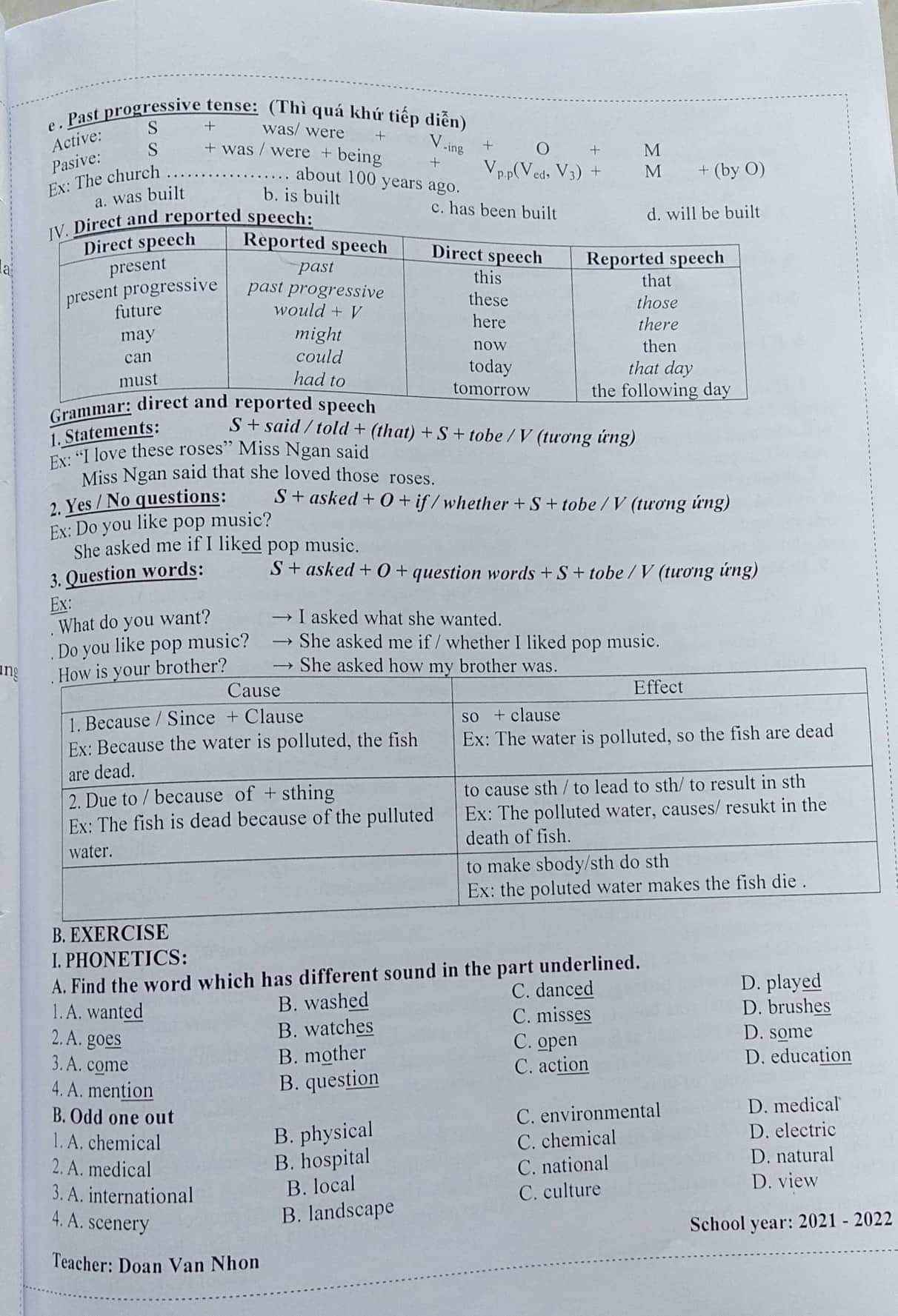





Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$