Giúp em bài 5 với 🙏🙏🙏
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 6 2023
5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP
NN
1
S
10 tháng 2 2023
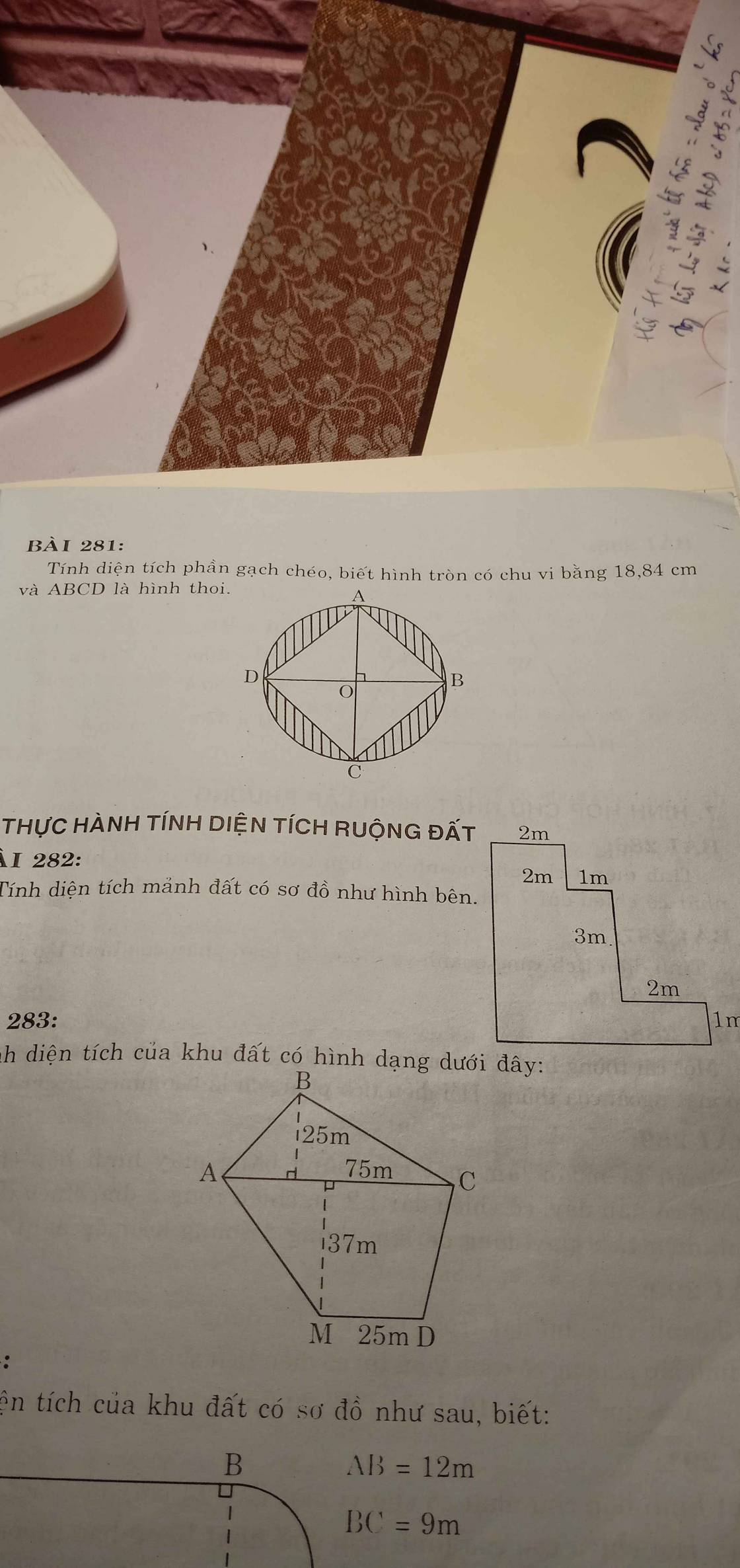
Bán kính hình tròn:
\(18,84:3,14:2=3\left(cm\right)\)
Diện tích hình tròn:
\(3\times3\times3,14=28,26\left(cm^2\right)\)
Đường kính hình tròn:
\(3\times2=6\left(cm\right)\)
Diện tích hình thoi:
\(\dfrac{6\times6}{2}=18\left(cm^2\right)\)
Diện tích phần gạch chéo:
\(28,26-18=10,26\left(cm^2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)
2 tháng 7 2023
4:
a: -90<a<0
=>cos a>0
cos^2a=1-(-4/5)^2=9/25
=>cosa=3/5
\(sin\left(45-a\right)=sin45\cdot cosa-cos45\cdot sina=\dfrac{\sqrt{2}}{2}\left(cosa-sina\right)\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{3}{5}-\dfrac{4}{5}\right)=\dfrac{-\sqrt{2}}{10}\)
b: pi/2<a<pi
=>cosa<0
cos^2a+sin^2a=0
=>cos^2a=16/25
=>cosa=-4/5
tan a=3/5:(-4/5)=-3/4
\(tan\left(a+\dfrac{pi}{3}\right)=\dfrac{tana+\dfrac{tanpi}{3}}{1-tana\cdot tan\left(\dfrac{pi}{3}\right)}\)
\(=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\dfrac{-3}{4}\cdot\sqrt{3}}=\dfrac{48-25\sqrt{3}}{11}\)
c: 3/2pi<a<pi
=>cosa>0
cos^2a+sin^2a=1
=>cos^2a=25/169
=>cosa=5/13
cos(pi/3-a)
\(=cos\left(\dfrac{pi}{3}\right)\cdot cosa+sin\left(\dfrac{pi}{3}\right)\cdot sina\)
\(=\dfrac{5}{13}\cdot\dfrac{1}{2}+\dfrac{-12}{13}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{5-12\sqrt{3}}{26}\)
VT
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
3.
Xét \(x^2-8x+7\le0\Leftrightarrow\left(x-1\right)\left(x-7\right)\le0\Rightarrow1\le x\le7\)
Có tập nghiệm \(D_1=\left[1;7\right]\)
Xét \(x^2-\left(2m+1\right)x+m^2+m\le0\Leftrightarrow\left(x-m\right)\left(x-m-1\right)\le0\)
\(\Leftrightarrow m\le x\le m+1\) có tập nghiệm là \(D_2=\left[m;m+1\right]\)
a. Hệ BPT vô nghiệm khi \(D_1\cap D_2=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m>7\\m+1< 1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>7\\m< 0\end{matrix}\right.\)
b. Do \(D_2\) là đoạn có độ dài bằng \(m+1-m=1\) nên hệ có tập nghiệm là 1 đoạn dài 1 trên trục số khi: \(D_2\subset D_1\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+1\le7\end{matrix}\right.\) \(\Rightarrow1\le m\le6\)
\(\dfrac{k.C_n^k}{C_n^{k-1}}=\dfrac{k.n!}{k!\left(n-k\right)!}.\dfrac{\left(k-1\right)!.\left(n-k+1\right)!}{n!}=n-k+1\)
Do đó:
\(S=2016-0+2016-1+...+2016-2015\)
\(=2016+2015+...+1=\dfrac{2016.2017}{2}=...\)