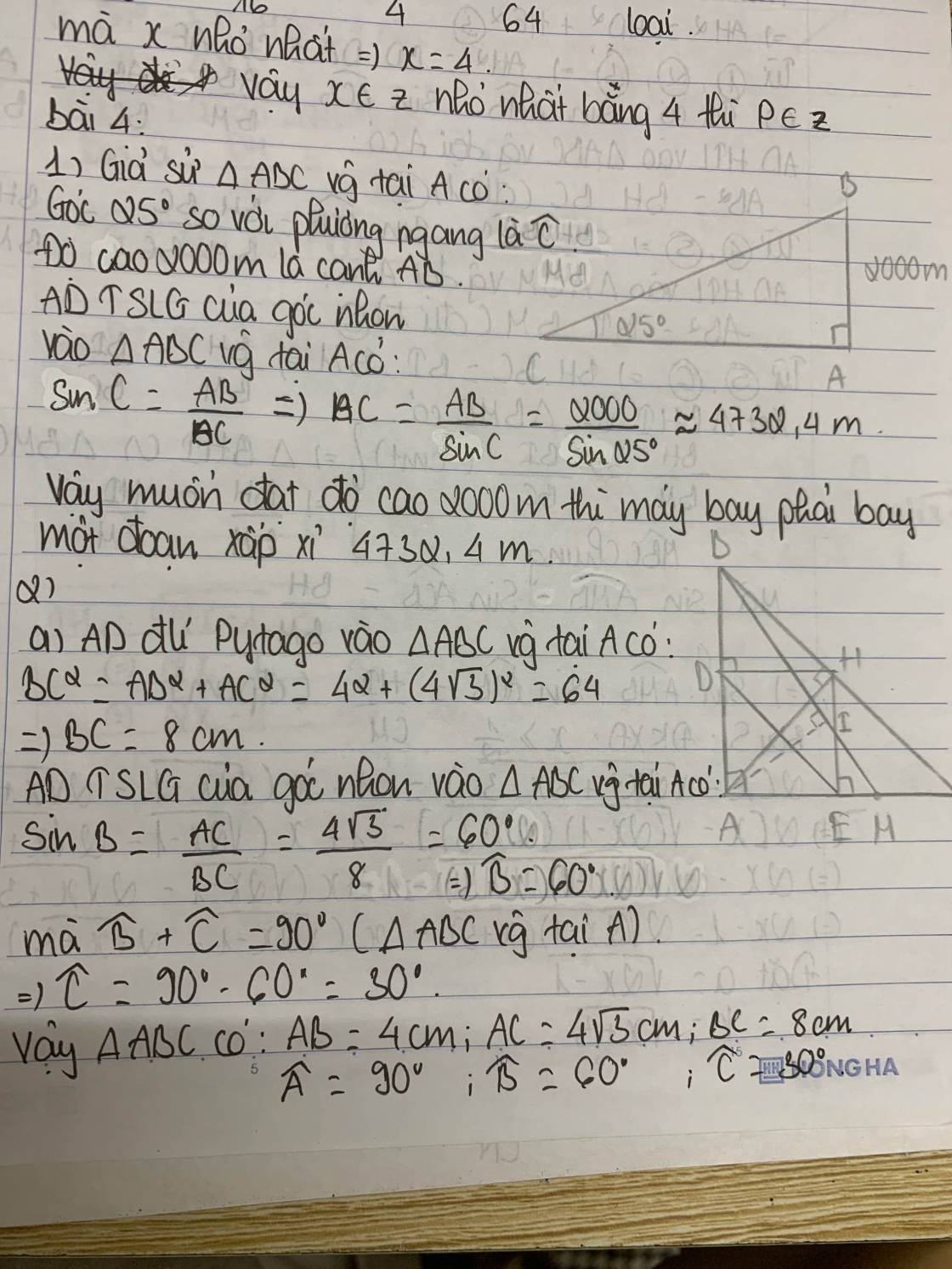1) Một chiếc máy bay cất cánh theo một góc $25^{\circ}$ so với phương ngang. Hỏi muốn đạt độ cao $2000 \mathrm{~m}$ thì máy bay phải bay một đoạn đường là bao nhiêu mét? (làm tròn kết quả đến chũ số thâp phân thứ nhất).
2) Cho tam giác $A B C$ vuông tại $A$, đường cao $A H$.
a)Biết $A B=4 \mathrm{~cm}, A C=4 \sqrt{3} \mathrm{~cm}$. Giải tam giác $A B C$.
b)Kẻ $H D, H E$ lần lượt vuông góc với $A B, A C$ ( $D$ thuộc $A B, E$ thuộc $A C$ ). Chứng minh $B D \cdot D A+C E \cdot E A=A H^2$.
c)Lấy điểm $M$ nằm giữa $E$ và $C$, kẻ $A I$ vuông góc với $M B$ tại $I$. Chứng minh $\sin \widehat{A M B} \cdot \sin \widehat{A C B}=\dfrac{H I}{C M}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ minh họa.
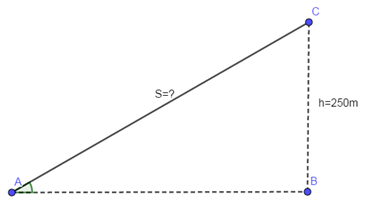
Độ dài đoạn AC chính là quãng đường máy bay cần đi để đạt độ cao 250m.
Xét tam giác ABC vuông tại B có:
sin(∠CAB)=BCAC⇒AC=BCsin(∠CAB)=hsin23o=250sin23o≈640(m)sin(∠CAB)=BCAC⇒AC=BCsin(∠CAB)=hsin23o=250sin23o≈640(m)
Vậy máy bay cần bay quãng đường 640 (m) để đạt được độ cao 250 (m).

Lời giải:
Đoạn đường máy bay phải đi là:
$2500:\sin 23^0=6398$ (mét)

Đổi 1,5’ = 1 40 h
Sau 1,5 phút máy bay ở C
Quãng đường bay được là BC = 480. = 12km và B ^ = 25 0
Nên AC = BC. sin 25 0 = 5,1km
Vậy máy bay đạt được độ cao là 5,1km sau 1,5 phút
Đáp án cần chọn là: C

Đổi 1,2’ = 1 50 h
Sau 1,2 phút máy bay ở C
Quãng đường bay được là BC = 500. 1 50 = 10km và B ^ = 30 0
Nên AC = BC. sin 30 0 = 5km
Vậy máy bay đạt được độ cao là 5km sau 1,2 phút
Đáp án cần chọn là: B

Hình vẽ bên minh họa một chiếc máy bay đang cất cánh từ sân bay. Đường bay lên tạo với phương nằm ngang một góc bằng 35 độ . Hỏi sau khi bay được quãng đường 10km thì máy bay ở độ cao bao nhiêu km so với mặt đất