35x-(-2)=46+33x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(37\times46+37\times51+111\)
\(=37\times46+37\times51+37\times3\)
\(=37\times\left(46+51+3\right)\)
\(=37\times100\)
\(=3700\)
b) \(35\times215-35\times210-175\)
\(=35\times215-35\times210-35\times5\)
\(=35\times\left(215-210-5\right)\)
\(=35\times0\)
\(=0\)
c) \(172\times47+86\times8-34\times4\)
\(=4\times\left(43\times47+86\times2-34\right)\)
\(=4\times\left(2021+172-34\right)\)
\(=4\times2159\)
\(=8636\)
d) \(48\times56+28\times104\)
\(=48\times56+56\times52\)
\(=56\times\left(48+52\right)\)
\(=56\times100\)
\(=5600\)




Ta có : \(6x^4-35x^3+62x^2-35x+6=0\)
=> \(6x^4-3x^3-32x^3+16x^2+46x^2-23x-12x+6=0\)
=> \(3x^3\left(2x-1\right)-16x^2\left(2x-1\right)+23x\left(2x-1\right)-6\left(2x-1\right)=0\)
=> \(\left(3x^3-16x^2+23x-6\right)\left(2x-1\right)=0\)
=> \(\left(3x^3-x^2-15x^2+5x+18x-6\right)\left(2x-1\right)=0\)
=> \(\left(x^2\left(3x-1\right)-5x\left(3x-1\right)+6\left(3x-1\right)\right)\left(2x-1\right)=0\)
=> \(\left(x^2-5x+6\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left(x^2-2x-3x+6\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left(x\left(x-2\right)-3\left(x-2\right)\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left(x-3\right)\left(x-2\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left[{}\begin{matrix}x-3=0\\x-2=0\\3x-1=0\\2x-1=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=3\\x=2\\x=\frac{1}{3}\\x=\frac{1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là \(S=\left\{2,3,\frac{1}{2},\frac{1}{3}\right\}\)
Nhận thấy \(x=0\) ko là nghiệm, chia 2 vế của pt cho \(x^2\)
\(6x^2+\frac{6}{x^2}-35x-\frac{35}{x}+62=0\)
\(\Leftrightarrow6\left(x^2+\frac{1}{x^2}\right)-35\left(x+\frac{1}{x}\right)+62=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(6\left(t^2-2\right)-35t+62=0\)
\(\Leftrightarrow6t^2-35t+50=0\Rightarrow\left[{}\begin{matrix}t=\frac{5}{2}\\t=\frac{10}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=\frac{5}{2}\\x+\frac{1}{x}=\frac{10}{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x^2-5x+2=0\\3x^2-10x+3=0\end{matrix}\right.\)


Cách giải:
lim x → - ∞ 4 x 2 + x - 1 - x 2 - x + 3 3 x + 2 = lim x → - ∞ - 4 + 1 x + 1 x 2 + 1 - 1 x + 3 x 2 3 + 2 x = - 2 + 1 3 = - 1 3

xin lỗi nhé mình mới có lớp 6 à nên ko bít
tha lỗi cho mình nhé!
\(\left(x^2+22x-120\right)\left(x^2+33x+270\right)-2x^2\)
\(=x^4+55x^3+876x^2+1980x-32400-2x^2\)
\(=x^4+55x^3+874x^2+1980x-32400\)
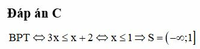
35x - (-2) = 46 + 33x
35x - 33x = (-2) + 46
2x = 44
x = 22
k mik nha bn
<=> 35x + 2 = 46 + 33x
<=> 35x - 33x = 46 - 2
<=> 2x = 44
<=> x = 44 : 2
<=> x = 22