
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

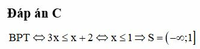

a) ĐK: x-1 khác 0 và x+1 khác 0
<=> x khác 1 và x khác -1
b) ĐK: x-2 khác 0
<=> x khác 2

a) -2x+14=0
<=>-2x= - 14
<=>x = 7
Vậy phương trình có tập nghiệm x={7}
b)(4x-10) (x+5)=0
<=>4x-10=0 <=>4x=10 <=>x=5/2
<=>x+5=0 <=>x=-5
Vậy phương trình có tập nghiệm x={5/2;- 5}
c)\(\frac{1-x}{x+1}\) + 3=\(\frac{2x+3}{x+1}\)
ĐKXD: x+1 #0<=>x#-1(# là khác)
\(\frac{1-x}{x+1}\)+3=\(\frac{2x+3}{x+1}\)
<=>\(\frac{1-x}{x+1}\)+\(\frac{3.\left(x+1\right)}{x+1}\)=\(\frac{2x+3}{x+1}\)
<=>\(\frac{1-x}{x+1}\)+\(\frac{3x+3}{x+1}\)=\(\frac{2x+3}{x+1}\)
=>1-x+3x+3=2x+3
<=>-x+3x-2x=-1-3+3
<=>0x = -1 (vô nghiệm)
Vâyj phương trình vô nghiệm
d) 1,2-(x-0,8)=-2(0,9+x)
<=> 1,2-x+0,8=-1,8-2x
<=>-x+2x=-1,2-0,8-1,8
<=>x=-4
Vậy phương trình có tập nghiệm x={-4}

Đáp án C
f ( t ) = t ( t 2 + 3 + 1 ) ⇒ f ' ( t ) = t 2 + 3 + 1 + t t t 2 + 3 > 0 ∀ t ( x + 2 ) ( ( x + 2 ) 2 + 3 + 1 ) > − x ( x 2 + 3 + 1 ) ⇔ ( x + 2 ) ( ( x + 2 ) 2 + 3 + 1 ) > − x ( ( − x ) 2 + 3 + 1 ) ⇔ f ( x + 2 ) > f ( − x ) ⇔ x + 2 > − x ⇔ x > − 1

Đáp án A
Điều kiện: x ≥ − 1 ta có hệ phương trình:
x + 1 < 2 x x + 4 < 2 x 2 + 3 ⇔ 2 x 2 − x − 1 < 0
nên ta có lập luận sau
Vế phải bất phương trình:
g x = 6 x 2 − 3 x − 3 = 3 2 x 2 − x − 1 ⇒ g x > 0 ⇔ x ∈ − ∞ ; − 1 2 ∪ 1 ; + ∞ g x ≤ 0 ⇔ x ∈ − 1 2 ; 1
+) Với x>1 thì:
0 < x + 4 < 2 x 2 + 3 0 < x + 1 < 2 x ⇒ x + 4 x + 1 < 2 x 2 x 2 + 3 ⇒ V T < 0 , V P > 0 ⇒ B P T v ô n g h i ệ m .
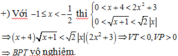
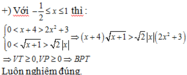
Vật tập nghiệm của bất phương trình là:
a ; b = − 1 2 ; 1 ⇒ 2 a + b = 2. − 1 2 + 1 = 0

Đáp án B.
TXĐ: x + 2 > 0 1 − x > 0 ⇔ − 2 < x < 1.
Bất phương trình tương đương với:
log 3 x + 2 1 − x ≥ 1 ⇔ x + 2 1 − x ≥ 3 ⇔ x + 2 ≥ 3 − 3 x ⇔ x ≥ 1 4 .
Do đó a = 1 4 ; b = 1 nên
S = 2 2 + 1 3 = 5.

Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .

a) \(4x-7>0\Leftrightarrow4x>7\)\(\Leftrightarrow x>\frac{7}{4}\)
b) \(-5x+8>0\Leftrightarrow5x<8\Leftrightarrow x<\frac{8}{5}\)
c)\(9x-10\le0\Leftrightarrow9x\le10\)\(\Leftrightarrow x\le\frac{10}{9}\)
d) \(\left(x+1\right)^2+4\le x^2+3x+10\)\(\Leftrightarrow x^2-2x+1+4\le x^2+3x+10\)
\(\Leftrightarrow5x\ge-5\Leftrightarrow x\ge-1\)
a,
4x - 7 > 0
↔ 4x > 7
↔ x > \(\dfrac{7}{4}\)
Vậy tập nghiệm của bất phương trình là S = { x / x>\(\dfrac{7}{4}\) }
b,
-5x + 8 > 0
↔ 8 > 5x
↔ \(\dfrac{8}{5}\) > x
Vậy tập nghiệm của bất phương trình là S = { x / \(\dfrac{8}{5}\) > x }
c,
9x - 10 ≤ 0
↔ 9x ≤ 10
↔ x ≤ \(\dfrac{10}{9}\)
Vậy tập nghiệm của bất phương trình là S = { x / x ≤ \(\dfrac{10}{9}\) }
d,
( x - 1 )\(^2\) + 4 ≤ x\(^2\) + 3x + 10
↔ x\(^2\) - 2x +1 +4 ≤ x\(^2\) + 3x + 10
↔ 1 + 4 - 10 ≤ x \(^2\) - x\(^2\) + 3x + 2x
↔ -5 ≤ 5x
↔ -1 ≤ x
Vậy tập nghiệm của bất phương trình là S = { x / -1 ≤ x}