Cho tam giác ABC vuông góc tại A. Trên AB,BC lần lượt lấy D,E. CMR CD2-BC2=ED2-BE2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
16 tháng 7 2021
a) đề phải là \(\dfrac{EB}{FC}=\dfrac{AB^3}{AC^3}\)
Ta có: \(\dfrac{EB}{FC}.\dfrac{AB}{AC}=\dfrac{BE.BA}{AC.CF}=\dfrac{BH^2}{CH^2}=\left(\dfrac{BH}{CH}\right)^2=\left(\dfrac{BH.BC}{CH.BC}\right)^2\)
\(=\left(\dfrac{AB^2}{AC^2}\right)^2=\dfrac{AB^4}{AC^4}\Rightarrow\dfrac{EB}{FC}=\dfrac{AB^3}{AC^3}\)
b) Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow AH^2=EF^2=EH^2+HF^2\)
Ta có: \(3AH^2+BE^2+CF^2=\left(BE^2+EH^2\right)+\left(CF^2+FH^2\right)+2AH^2\)
\(=BH^2+CH^2+2.BH.CH=\left(BH+CH\right)^2=BC^2\)
NM
0
W
15 tháng 2 2020
a) Xét tam giác MBD vuông tại D và tam giác NCE vuông tại E có:
BM=CN(gt)
\(\widehat{B}=\widehat{C}\)(tam giác ABC cân)
Suy ra \(\Delta MBD=\Delta NCE\)(cạnh huyền-góc nhọn)
=>EC=BD(2 cạnh tương ứng)
b) Xét tam giác ADB và tam giác ACE có:
\(\widehat{B}=\widehat{C}\)(tam giác ABC cân)
AB=AC(tam giác ABC cân)
EC=BD(cmt)
Suy ra \(\Delta ADB=\Delta ACE\)(c.g.c)
=>AD=AE(2 cạnh tương ứng)
15 tháng 2 2020
a, xét tam giác BDM và tam giác CEN có :
góc BDM = góc CEN = 90
BM = NC (Gt)
góc ABC = góc ACB do tam giác ABC cân tại A (Gt)
=> tam giác BDM = tam giác CEN (ch-gn)
b, tam giác BDM = tam giác CEN (câu a)
=> góc BMD = góc CNE (đn)
góc BMD + góc DMA = 180 (kb)
góc CNE + góc ENA = 180 (kb)
=> góc DMA = góc ENA (1)
có AB = AC do tam giác ABC cân tại A (gt)
BM = CN (gt)
BM + MA = AB
CN + NA = AC
=> MA = NA (2)
xét tam giác DMA và tam giác ENA có MD = EN do tam giác BDM = tam giác CEN (câu a)
(1)(2)
=> tam giác DMA = tam giác ENA (c-g-c)
=> AD = AE (đn)
23 tháng 11 2023
a: Xét ΔBEM vuông tại M có \(\widehat{B}=45^0\)
nên ΔBEM vuông cân tại M
b: ME\(\perp\)BC
NF\(\perp\)BC
Do đó: ME//NF
Xét ΔCNF vuông tại N có \(\widehat{NCF}=45^0\)
nên ΔCNF vuông cân tại N
=>CN=NF
CN=NF
BM=ME
CN=NM=MB
Do đó: CN=NF=BM=ME=NM
Xét tứ giác NMEF có
NF//ME
NF=ME
Do đó: NMEF là hình bình hành
Hình bình hành NMEF có NM=NF
nên NMEF là hình thoi
Hình thoi NMEF có \(\widehat{FNM}=90^0\)
nên NMEF là hình vuông
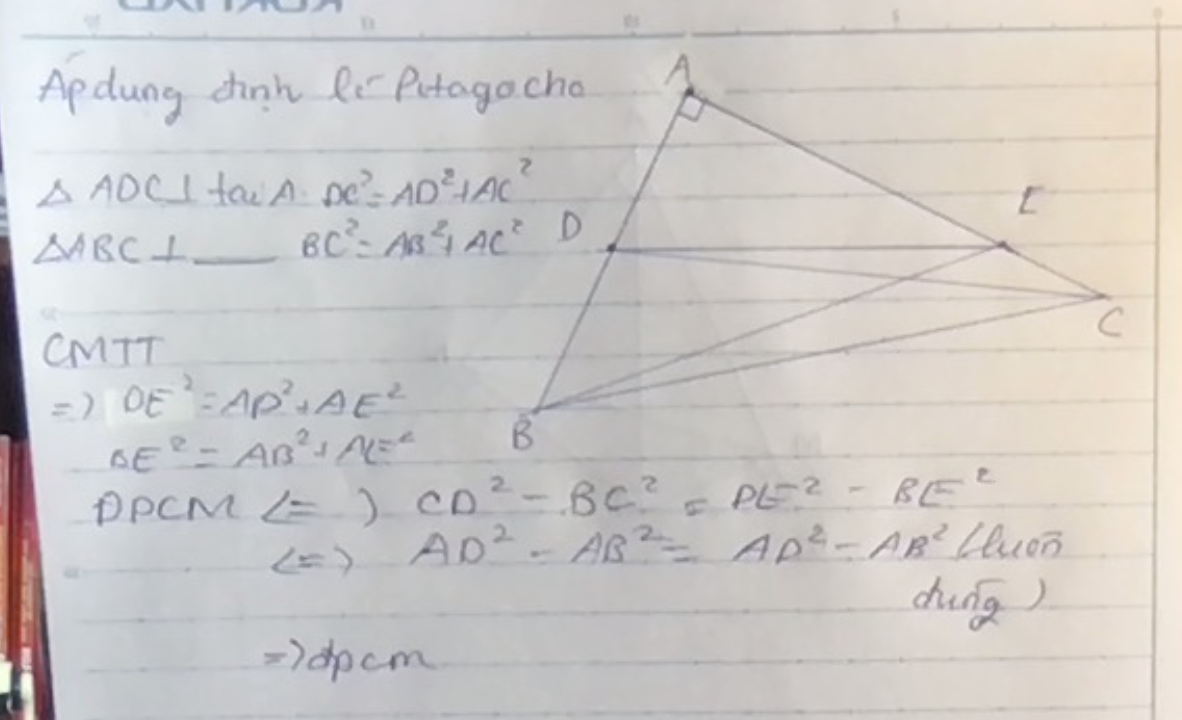
Cho tam giác ABC vuông góc tại A. Trên AB,BC lần lượt lấy D,E. CMR CD2-BC2=ED2-BE2