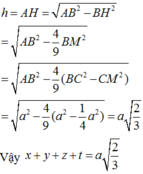Cho tứ giác ABCD và điểm M là 1 điểm nằm trong tứ giác đó. Xác địng vị trí của M để:
a) Tổng các khoảng cách từ điểm đó đến các đỉnh của tứ giác là nhỏ nhất
b) Tổng các khoảng cách từ điểm đó đến các cạnh của tứ giác là lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là giao điểm của AC và BD
TH1: M trùng O
=> AM+MB+MC+AD=AC+BD(1)
TH2: M không trùng O
Áp dụng BĐT tam giác, ta có:
\(\hept{\begin{cases}AM+MC>AC\\MB+MD>BD\end{cases}\Rightarrow AM+MB+MC+MD>AC+BD}\)(2)
Từ (1)và (2) => để tổng khoảng cách từ M đến cách đỉnh trong tứ giác ABCD nhỏ nhất => M trùng O

L=MA+MB+MC+MD
L=(MA+MD)+(MB+MC)
(MA+MD) nhỏ nhất khi AMD trên đường thẳng
(MB+MC) nhỏ nhất khi BMC trên đường thẳng
=> Lmin đạt được khi M là giao hai đường chéo AD và BC

Ta có : \(MA+MC\ge AC\)
Dấu " = " xảy ra khi M thuộc AC
Ta có :\(MB+MD\ge BD\)
\(\Rightarrow MA+MC+MB+MD\ge AC+BD\)
Dấu " = " xảy ra khi M là giao điểm của AC, BD
Vậy khi M là giao điểm của AC và BD thì MA+MB+MC+MD nhỏ nhất
Theo đề bài ta có :\(MA+MC\ge AC\)
Dấu " = " xảy ra khi và chỉ khi \(M\in AC\)
Theo đề bài có : \(MB+MD\ge BD\)
Dấu " =" xảy ra khi và chỉ khi \(M\in BD\)
\(\Rightarrow MA+MB+MC+MD\ge AC+BD\)
Vậy \(MA+MB+MC+MD\)nhỏ nhất sẽ bằng \(AC+BD\)
\(\Leftrightarrow\)M là giao điểm của 2 đường chéo AC và BD .

với tam giác ABC , cho góc B và góc C là góc nhọn
gọi d là tổng khoảng cách từ B và C đến đường thẳng AM, BD vuông góc AM , AH vuông góc BC..
ta có : giá trị lớn nhất của d = BC
<=> BD=BM ; CE=CM
<=> D trùng với M và E trùng với M
<=> M trùng với hình chiếu H của A trên BC
Vậy vị trí của M để có tổng các khoảng cách từ B và C đến AM lớn nhất là khi M trùng với hình chiếu H của A trên BC.

Chọn B.
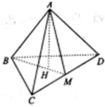
Gọi x, y, z, t lần lượt là khoảng cách từ M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Ta có

Cộng lại ta thu được (chú ý rằng)
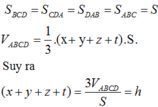
với h là độ dài đường cao của tứ diện đều ABCD. Ta có