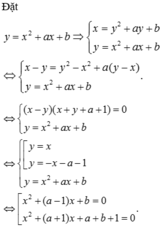tìm số thực a để phương trình sau có nghiệm nguyên: x2 - ax + a + 2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 3 2019
Chọn đáp án B
Gọi x 0 là nghiệm thực chung của 2 phương trình
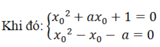
⇒ x 0 2 + a x 0 + 1 = x 0 2 - x 0 - a ⇔ (a + 1) x 0 = -(a + 1) ⇔ x 0 = -1
Thay x 0 = -1 vào phương trình x 0 2 + a x 0 + 1 = 0 tìm được a = 2
25 tháng 9 2021
Ta có: \(\left(\sqrt{2}\right)^2+a\cdot\sqrt{2}+b=0\)
\(\Leftrightarrow a\sqrt{2}+b=-2\)
Vì b là số nguyên
và -2 cũng là số nguyên
nên \(a\sqrt{2}\) cũng là số nguyên(vô lý)
25 tháng 9 2021
\(x^2+ax+b=0\) có nghiệm là \(\sqrt{2}\) nên
\(2+a\sqrt{2}+b=0\\ \Leftrightarrow b=a\sqrt{2}\)
Mà \(a,b\in Z\) nên đẳng thức xảy ra khi: \(a=b=0\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
\(\Delta=a^2+8>0\Rightarrow\) pt luôn có 2 nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=a\\x_1x_2=-2\end{matrix}\right.\)
\(N=x_1^2+x_2^2+x_1x_2+2\left(x_1+x_2\right)+4\)
\(=\left(x_1+x_2\right)^2-x_1x_2+2\left(x_1+x_2\right)+4\)
\(=a^2+2+2a+4\)
\(N=a^2+2a+6=\left(a+1\right)^2+5\ge5\)
\(N_{min}=5\) khi \(a=-1\)
4 tháng 6 2023
a: Δ=(-2m)^2-4(2m-3)
=4m^2-8m+12
=4m^2-8m+4+8=(2m-2)^2+8>0 với mọi m
=>PT luôn có hai nghiệm pb
b: PT có hai nghiệm trái dấu
=>2m-3<0
=>m<3/2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
Do pt có 1 nghiệm là \(2-\sqrt{3}\)
\(\Rightarrow\left(2-\sqrt{3}\right)^2+a\left(2-\sqrt{3}\right)+b=0\)
\(\Leftrightarrow7-4\sqrt{3}+2a-a\sqrt{3}+b=0\)
\(\Leftrightarrow2a+b+7=\left(a+4\right)\sqrt{3}\)
Vế trái là số hữu tỉ, vế phải vô tỉ nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}a+4=0\\2a+b+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-4\\b=1\end{matrix}\right.\)
CM
23 tháng 8 2017
Đáp án D
Ta có lim x → 2 − f x = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − − 2 x − 3 = − 1
Và lim x → 2 − f x = lim x → 2 − a + 1 − x 2 + x = a − 1 4 ; f 2 = a − 1 4 .
Theo bài ra, ta có lim x → 2 + f x = lim x → 2 − f x = f 2 ⇒ a = − 3 4
Do đó, bất phương trình − x 2 + a x + 7 4 > 0 ⇔ − x 2 − 3 4 x + 7 4 > 0 ⇔ − 7 4 < x < 1.
BM
1
30 tháng 11 2018
PT có nghiệm chung khi \(x^2+ax+8=x^2+x+a\)
\(\Leftrightarrow ax+8-x-a=o\)
\(\Leftrightarrow a\left(x-1\right)-\left(x-1\right)+7=0\)
\(\Leftrightarrow\left(x-1\right)\left(a-1\right)=-7\)
-7=(-1).7=(-7).1
TH1\(\hept{\begin{cases}x-1=-1\\a-1=7\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\a=8\end{cases}}\)thế vào \(x^2+x+a=0\)(thế vào pt trên cx đc nha) có: 8=0(vô lý) loại
TH2 \(\hept{\begin{cases}x-1=-7\\a-1=1\end{cases}}\)(giải như trên) (loại)
TH3\(\hept{\begin{cases}x-1=7\\a-1=-1\end{cases}}\)(loại)
Th4\(\hept{\begin{cases}x-1=1\\a-1=-7\end{cases}}\)=>\(\hept{\begin{cases}x=2\\a=-6\end{cases}}\)thế vào \(x^2+x+a=0\) có \(2^2+2-6=0\) thỏa mãn
Vậy với a=-6 thì 2 pt có nghiệm chng