Giải giúp mình vớiii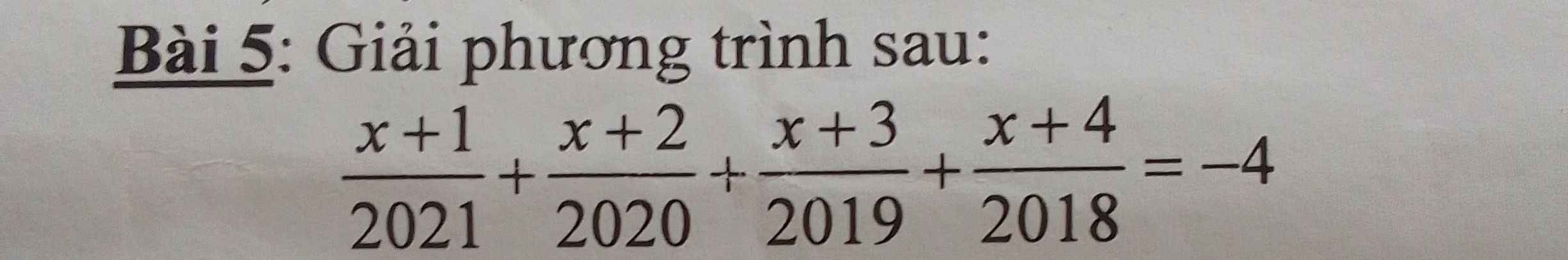
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 3 2022
a: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH∼ΔBDA
b: Xét ΔHAD vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\)
Do đó: ΔHAD∼ΔHBA
Suy ra: HA/HB=HD/HA
hay \(HA^2=HB\cdot HD\)
11 tháng 3 2022
a) Xét \(\Delta ADH\) và \(\Delta BDA:\)
\(\widehat{H}=\widehat{A}\left(=90^o\right).\)
\(\widehat{D}\) chung.
\(\Rightarrow\Delta ADH\sim\Delta BDA\left(g-g\right).\)
b) Xét \(\Delta BDA\) và \(\Delta BAH:\)
\(\widehat{BAD}=\widehat{BHA}\left(=90^o\right).\)
\(\widehat{B}\) chung.
\(\Rightarrow\Delta BDA\sim\) \(\Delta BAH\left(g-g\right).\)
Mà \(\Delta ADH\sim\Delta BDA\left(cmt\right).\)
\(\Rightarrow\Delta ADH\sim\Delta BAH.\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{DH}{AH}\) (2 cạnh tương ứng).
\(\Rightarrow AH^2=DH.BH.\)
6 tháng 2 2022
= (12-12) + (11+10) - (9+8) - (7+5) - (4+3) + (2-1)
= 0 + 21 - 17 - 12 - 7 + 1
= 21- 17 - 12 - 7 +1
= 4 - 12 - 7 +1
= -8 - 7 + 1
= -15 + 1
= -14
hết
7 tháng 2 2022
= 12 - 12 + 11 + ( 10 - 9 ) + ( 8 - 7 ) + ( 5 - 4 ) + 3 + ( 2 -1 )
= 0 + 11 + 1 + 1 + 1 + 3 + 1
= 11 +1 + 1 + 1 + 3 + 1
= 12 + 1 + 1 + 3 + 1
= 13 + 1 + 3 + 1
= 14 + 3 + 1
= 17 + 1
= 18
Đáp án đây nha bạn !!!
Chúc bạn học tốt !!!
15 tháng 8 2021
\(B=\left|x+1\right|+\left|x-4\right|+\left|2x-5\right|\ge\left|2x-3\right|+\left|2x-5\right|=\left|2x-3\right|+\left|5-2x\right|\)
\(\ge\left|2x-3+5-2x\right|=\left|2\right|=2\)
Dấu ''='' xảy ra khi \(\left(x+1\right)\left(4-x\right)\ge0;\left(2x-3\right)\left(5-2x\right)\ge0\)
\(-1\le x\le4;\frac{3}{2}\le x\le\frac{5}{2}\Rightarrow-1\le x\le4\)
Vậy GTNN của B bằng 2 tại -1 =< x =< 4
26 tháng 3 2023
a)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
b) \(n_{C_2H_4}=\dfrac{6}{22,4}=\dfrac{15}{56}\left(mol\right)\)
Theo PTHH: \(n_{CO_2}=\dfrac{15}{28}\left(mol\right)\Rightarrow V_{CO_2}=\dfrac{15}{28}.22,4=12\left(l\right)\)
NH
0
6 tháng 12 2021
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
17 tháng 12 2021
Câu 2:
c: 18 công nhân hoàn thành trong:
21x12:18=14(ngày)
`[x+1]/2021+[x+2]/2020+[x+3]/2019+[x+4]/2018=-4`
`<=>[x+1]/2021+1+[x+2]/2020+1+[x+3]/2019+1+[x+4]/2018+1=-4+4`
`<=>[x+1+2021]/2021+[x+2+2020]/2020+[x+3+2019]/2019+[x+4+2018]/2018=0`
`<=>[x+2022]/2021+[x+2022]/2020+[x+2022]/2019+[x+2022]/2018=0`
`<=>(x+2022)(1/2021+2020+1/2019+1/2018)=0`
Mà `1/2021+2020+1/2019+1/2018 \ne 0`
`=>x+2022=0`
`<=>x=-2022`
Vậy `S={-2022}`
Cảm ơn bạn