Cho các phân số \(\dfrac{3}{4}\);\(\dfrac{7}{7}\);\(\dfrac{3}{2}\);\(\dfrac{4}{3}\)phân số nào lớn nhất trong các phân số đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,A=\dfrac{-3\left(2n-3\right)-8}{2n-3}=-3-\dfrac{8}{2n-3}\in Z\\ \Leftrightarrow2n-3\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\\ \Leftrightarrow n\in\left\{1;2\right\}\left(n\in Z\right)\)
\(b,\dfrac{ab}{a+2b}=\dfrac{3}{2}\Leftrightarrow\dfrac{a+2b}{ab}=\dfrac{2}{3}\Leftrightarrow\dfrac{1}{b}+\dfrac{2}{a}=\dfrac{2}{3}\\ \dfrac{bc}{b+2c}=\dfrac{4}{3}\Leftrightarrow\dfrac{b+2c}{bc}=\dfrac{3}{4}\Leftrightarrow\dfrac{1}{c}+\dfrac{2}{b}=\dfrac{3}{4}\\ \dfrac{ca}{c+2a}=3\Leftrightarrow\dfrac{c+2a}{ca}=\dfrac{1}{3}\Leftrightarrow\dfrac{1}{a}+\dfrac{2}{c}=\dfrac{1}{3}\)
Cộng vế theo vế \(\Leftrightarrow\dfrac{3}{a}+\dfrac{3}{b}+\dfrac{3}{c}=\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{1}{3}=\dfrac{7}{4}\)
\(\Leftrightarrow3\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{7}{4}\\ \Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{7}{12}\\ \Leftrightarrow\dfrac{ab+bc+ca}{abc}=\dfrac{7}{12}\\ \Leftrightarrow T=\dfrac{12}{7}\)

a) \(\dfrac{2}{5}=\dfrac{1}{5}\cdot\dfrac{2}{1}\)
\(\dfrac{15}{12}=\dfrac{5}{4}=\dfrac{5}{2}\cdot\dfrac{1}{2}\)
\(\dfrac{5}{-12}=\dfrac{-5}{12}=\dfrac{-5}{3}\cdot\dfrac{1}{4}\)
\(\dfrac{-3}{-4}=\dfrac{3}{4}=\dfrac{3}{2}\cdot\dfrac{1}{2}\)

I. Trắc nghiệm:
Câu 1: Trong các cách viết sau đây, cách viết nào không cho ta phân số?
A. 0,5−40,5−4 B. 313313 C. 0808 D. 1−91−9
Câu 2: Các số sau, cách viết nào cho ta phân số.
A. 2,342,34 B. −35−35 C. −2,34,5−2,34,5 D. 9090
Câu 3: Số nghịch đảo của −47−47 là:
A. −47−47 B. 4747 C. 7474 D. −74−74
Câu 4: Khi rút gọn phân số −27

a: Các số biểu diễn dưới dạng thập phân hữu hạn là
\(3\dfrac{1}{4}=3,25\)
\(\dfrac{7}{32}=0.21875\)

+ Các phân số 3/4 ; 5/8 ; 4/3 ; 2/3 theo thứ tự từ bé đến lớn là: 5/8 ; 2/3 ; 3/4 ; 4/3
+ Các phân số 3/7 ; 8/14 ; 3/8 ; 8/7 theo thứ tự từ lớn đến bé là: 8/7 ; 8/14 ; 3/7 ; 3/8

Tham khảo:
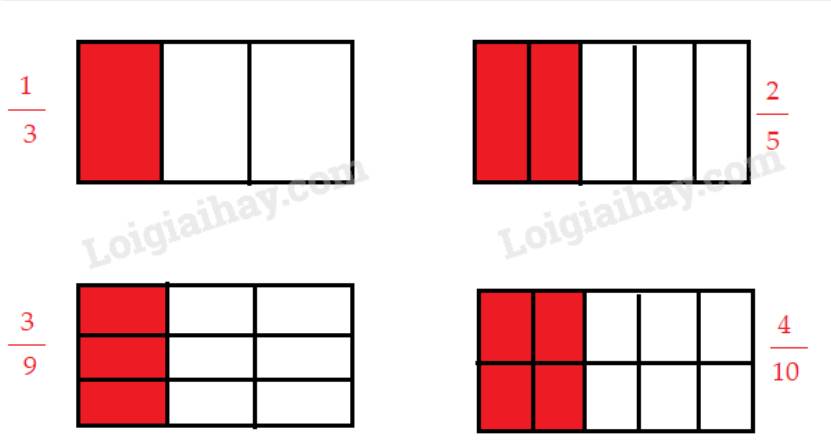
Như vậy,\(\dfrac{2}{5} = \dfrac{4}{{10}}\)
\(\dfrac{1}{3} = \dfrac{3}{9}\)
3/2
\(\dfrac{3}{2}\) lớn nhất vì các phân số còn lại < 1