Đang cần gấp
A/4.3x-12.3x+2=4.36+2.39
B/1/5.2x+1/3.2x+1=1/5.27+1/3.28
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
\(c,=x^4+2x^2+1-x^2=\left(x^2+1\right)-x^2=\left(x^2+x+1\right)\left(x^2-x+1\right)\)
GN
2
HP
7 tháng 2 2022
\(a.\dfrac{3}{2}+\dfrac{-1}{3}< \dfrac{x}{6}< \dfrac{1}{9}+\dfrac{31}{18}\)
\(\Leftrightarrow\dfrac{7}{6}< \dfrac{x}{6}< \dfrac{11}{6}\)
\(\Leftrightarrow7< x< 11\)
\(\Leftrightarrow x\in\left\{8;9;10\right\}\)
\(b.\dfrac{-5}{12}+\dfrac{7}{12}+\dfrac{-1}{12}< \dfrac{x}{12}< \dfrac{2}{15}+\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{1}{12}< \dfrac{x}{12}< \dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{1}{12}< \dfrac{x}{12}< \dfrac{4}{12}\)
\(\Leftrightarrow1< x< 4\)
\(\Leftrightarrow x\in\left\{2;3\right\}\)
CM
1 tháng 10 2018
Đáp án D
Phương pháp: Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình
Cách giải:
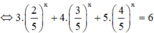
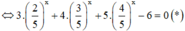
Hàm số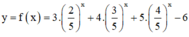 
nghịch biến trên R => f(x) = 0 có nhiều nhất 1 nghiệm trên R(1)
Ta có: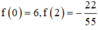 
có ít nhất 1 nghiệm 
Từ (1), (2) suy ra: phương trình đã cho có duy nhất một nghiệm thực
a: =>\(4\cdot3^x\cdot\dfrac{1}{3}+2\cdot3^x\cdot9=4\cdot3^6+2\cdot3^9\)
=>3^x(4*1/3+2*9)=3^6(4+2*3^3)
=>3^x*58/3=3^6*58
=>3^x/3^6=3
=>x-6=1
=>x=7
b: =>\(2^x\cdot\left(\dfrac{1}{5}+\dfrac{1}{3}\cdot2\right)=2^7\left(\dfrac{1}{5}+\dfrac{1}{3}\cdot2\right)\)
=>2^x=2^7
=>x=7