Cho tam giác ABC có góc B=2.góc C, AB=4cm, AC=8cm.Tính BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

Ta có: \(cos\left(B\right)=\dfrac{AB}{BC}\)
\(\Rightarrow cos\left(30^o\right)=\dfrac{AB}{8}\Rightarrow AB=cos\left(30^o\right)\cdot8\approx6,9\left(cm\right)\)
Ta có tam giác ABC vuông tại A áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AC^2}=\sqrt{8^2-6,9^2}\approx4\left(cm\right)\)

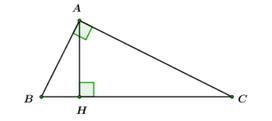
+) Chứng minh tam giác ABC vuông
Ta có:
+) Tính số đo B, C và độ dài đường cao AH của ABC
Áp dụng tỉ số lượng giác của góc nhọn trong ABC và có đường cao AH ta có:
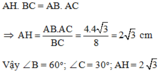
Đáp án cần chọn là: D


vì góc B = 2 góc C
=> AC = 2 AB ( quan hệ giữa góc và cạnh )
mà AB = 4 cm
=> AC = 2 x 4 =8 ( cm )
Vậy AC = 8cm
kẻ BD là phân giác của góc ABC
=>góc DBC=góc DCB
Xét ΔABD và ΔACB có
góc ABD=góc ACB
góc A chung
=>ΔABD đồng dạng với ΔACB
=>AD/AB=AB/AC
=>AD/4=4/8=1/2
=>AD=2cm
=>CD=6cm
BD là phân giác
=>AB/AD=BC/CD
=>BC/6=4/2=2
=>BC=12cm