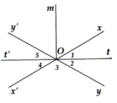
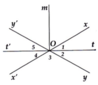
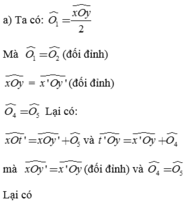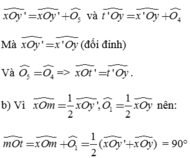Bài 1 : cho 2 đường thẳng xx' và yy' cắt nhau tại O , vẽ tia phân giác Ot của góc xOy .
A) Gọi Ot' là tia đối của tia Ot so sánh góc xOt' và góc t'Oy
B) vẽ tia phân giác Om của góc x'Oy . Tính góc mOt
Bài 2 : Cho góc xOy bằng 130° ở phía ngoài của góc vẽ 2 tia Oz , Ot sao cho Oz vuông góc Ox , Ot vuông góc Oy . Gọi Om là tia phân giác của góc xOy và Om' là tia đối của tia Om
A) CM Om' là tia phân giác của góc zOt
B) so sánh 2 góc mOz và góc yOm'