Một cái bơm chứa 20 cm3 không khí ở nhiệt độ 170C và áp suất 2.105 Pa. Khi không khí bị nén xuống còn 10 cm3 và nhiệt độ tăng lên tới 1270 C thì áp suất của không khí trong bơm là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2021
T1 = 27 + 273 = 300K
T2 = 327 + 273 = 600K
Phương trình trạng thái khí lí tưởng:
\(\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\Rightarrow\dfrac{10^5.120}{300}=\dfrac{P_2.20}{600}\Leftrightarrow\dfrac{12000000}{300}=\dfrac{20P_2}{600}\)
=> 20P2 = 24000000
=> P2 = 1200000Pa
S
6 tháng 4 2021
phương trình trạng thái lí tưởng:
\(\dfrac{P_1.V_1}{T_1}=\dfrac{P_2.V_2}{T2}\)
Theo đề bài:
V1 = 120cm3; T1 = 27 + 273 = 300K ; P1 = \(10^5\)Pa
V2 = 20cm3; T2 = 327 + 273 = 600K
Thay vào phương trình:
\(\dfrac{10^5.120}{300}=\dfrac{P_2.20}{600}\Rightarrow P_2=\dfrac{P_1.T_2.V_2}{V_2.T_1}=1200000Pa\)
=12.10^5 Pa
10 tháng 5 2022
\(\left\{{}\begin{matrix}p_1=10^5Pa\\V_1=80cm^3\\T_1=300^oK\end{matrix}\right.\\ \left\{{}\begin{matrix}p_2=?\\V_2=20cm^3\\T_2=600^oK\end{matrix}\right.\\ \dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Leftrightarrow\dfrac{10^5.80}{300}=\dfrac{p_2.20}{600}\\ \Rightarrow p_2=8.10^5Pa\)
SS
26 tháng 4 2016
1/ Quá trình biến đổi trạng thái khi thể tích không đổi gọi là đẳng tích
Định luật: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối
Biểu thức:
\(\frac{P}{T}=\) hằng số
+Lưu ý: Nếu gọi \(P_1,T_1\) là áp suất và nhiệt độ tuyệt đối của 1 lượng khí ở trạng thái 1
Nếu gọi \(P_2,T_2\) là áp suất và nhiệt độ tuyệt đối của 1 lượng khí ở trạng thái 2
Ta có biểu thức: \(\frac{P_1}{T_1}=\frac{P_2}{T_2}\)
2/ Phương trình trạng thái khí lí tưởng:
\(\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}\)
Tính ra \(p_2=2,58atm\)
VT
13 tháng 7 2018
Đáp án A.
p 1 V 1 = p 2 V 2 ⇒ 10 5 0 , 125.20.2 , 5 = p 2 .2 , 5 ⇒ p 2 = 2.10 5 P a
VT
23 tháng 1 2018
Đáp án: C
Ta có:
Thể tích khí bơm được sau 20 lần bơm là 20.0,125 lít
+ Thể tích của không khí trước khi bơm vào bóng: V 1 = 20.0,125 + 2,5 = 5 l (Bao gồm thể tích khí của 20 lần bơm và thể tích khí của khí có sẵn trong bóng)
+ Sau khi bơm khí vào trong bóng thể tích lượng khí chính bằng thể tích của bóng: V 2 = 2,5 l
Do nhiệt đọ không đổi, theo định luật Bôi lơ – Ma ri ốt, ta có:
p 1 V 1 = p 2 V 2 ⇔ 10 5 .5 = p 2 .2,5 ⇒ p 2 = 2.10 5 P a
DT
21 tháng 2 2022
cu ap dung cong thuc la ra, giai:
Xét lượng khí trong xi lanh.
Áp dụng định luật Bôilơ – Mariốt ta có:
\(p_1V_1=p_2V_2\Rightarrow p_2=\dfrac{p_1V_1}{V_2}=\dfrac{3.10^5.200}{100}=600000\left(Pa\right)\)
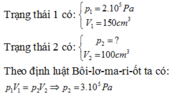
Trạng thái 1: \(\left\{{}\begin{matrix}p_1=2\cdot10^5Pa\\V_1=20cm^3\\T_1=17^oC=290K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=???\\V_2=10cm^3\\T_2=127^oC=400K\end{matrix}\right.\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Rightarrow\dfrac{20\cdot2\cdot10^5}{290}=\dfrac{p_2\cdot10}{400}\)
\(\Rightarrow p_2=5517241,4Pa\)