Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}p_1=10^5Pa\\V_1=80cm^3\\T_1=300^oK\end{matrix}\right.\\ \left\{{}\begin{matrix}p_2=?\\V_2=20cm^3\\T_2=600^oK\end{matrix}\right.\\ \dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Leftrightarrow\dfrac{10^5.80}{300}=\dfrac{p_2.20}{600}\\ \Rightarrow p_2=8.10^5Pa\)

Trạng thái 1: \(\left\{{}\begin{matrix}p_1=2\cdot10^5Pa\\V_1=20cm^3\\T_1=17^oC=290K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=???\\V_2=10cm^3\\T_2=127^oC=400K\end{matrix}\right.\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Rightarrow\dfrac{20\cdot2\cdot10^5}{290}=\dfrac{p_2\cdot10}{400}\)
\(\Rightarrow p_2=5517241,4Pa\)

1/ Quá trình biến đổi trạng thái khi thể tích không đổi gọi là đẳng tích
Định luật: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối
Biểu thức:
\(\frac{P}{T}=\) hằng số
+Lưu ý: Nếu gọi \(P_1,T_1\) là áp suất và nhiệt độ tuyệt đối của 1 lượng khí ở trạng thái 1
Nếu gọi \(P_2,T_2\) là áp suất và nhiệt độ tuyệt đối của 1 lượng khí ở trạng thái 2
Ta có biểu thức: \(\frac{P_1}{T_1}=\frac{P_2}{T_2}\)
2/ Phương trình trạng thái khí lí tưởng:
\(\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}\)
Tính ra \(p_2=2,58atm\)

Gọi số quả bóng bay bơm được là \(n\left(quả\right)\)
Trạng thái đầu:
\(\left\{{}\begin{matrix}V_1=50l\\p_1=5MPa=5\cdot10^6Pa\\T_1=37^oC=310K\end{matrix}\right.\)
Trạng thái sau:
\(\left\{{}\begin{matrix}V_2=10n+50\left(l\right)\\p_2=1,05\cdot10^5Pa\\T_2=12^oC=285K\end{matrix}\right.\)
Phương trình trạng thái khí lí tưởng: \(\dfrac{p_1\cdot V_1}{T_1}=\dfrac{p_2\cdot V_2}{T_2}\)
\(\Rightarrow\dfrac{5\cdot10^6\cdot50}{310}=\dfrac{\left(10n+50\right)\cdot1,05\cdot10^5}{285}\)
\(\Rightarrow n=213quả\)

Gọi số quả bóng bay bơm được là \(n\left(quả\right)\).
Trạng thái 1: \(\left\{{}\begin{matrix}p_1=5\cdot10^6Pa\\V_1=50l\\T_1=37^oC=310K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=1,05\cdot10^5Pa\\V_2=10n+50\left(l\right)\\T_2=12^oC=285K\end{matrix}\right.\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Rightarrow\dfrac{5\cdot10^6\cdot50}{310}=\dfrac{\left(1,05\cdot10^5\right)\cdot\left(10n+50\right)}{285}\)
\(\Rightarrow n\approx214quả\)

+Ta có 2,5 lít = 2,5 dm3 = 2,5.10-3 (m3). Đó là thể tích lúc sau.
+Còn thể tích lúc đầu là đây, bạn có mỗi lần bơm là 125 (cm3), thì sau 45 lần bơm, ta được 5625 cm3 = 5.625.10-3 (m3); 5.625.10-3 đó là thể tích lúc đầu đó bạn, tại sao ? Tại vì nếu thể tích bình lúc đầu là 2,5 lít thì nếu ta bơm thêm vào 5.625.10-3 thì nó đã bị nén, bạn phải biết, khi nén thì thể tích đầu phải lớn hơn thể tích sau nha.
+Áp dụng Định luật Bôi- lơ Ma-ri-ốt: p1.V1 = p2. V2
<=> 105. 5,625.10-3 = 2,5.10-3 . p2
<=> p2 = 225000 Pa
Sau 45 lần bơm đã đưa vào bóng một lượng khí ở bên ngoài có thể tích là V1 = 45 . 125 = 5625 cm3 và áp suất p1 = 105 pa
Khi vào trong quả bóng, lượng khí này có thể tích V2 = 2,5 lít = 2 . 500 cm3 và áp suất P2
Do nhiệt độ không đổi:
p1V1 = p2V2 => P2 = =
P2 = 2,25 . 105 Pa.
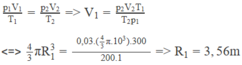
T1 = 27 + 273 = 300K
T2 = 327 + 273 = 600K
Phương trình trạng thái khí lí tưởng:
\(\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\Rightarrow\dfrac{10^5.120}{300}=\dfrac{P_2.20}{600}\Leftrightarrow\dfrac{12000000}{300}=\dfrac{20P_2}{600}\)
=> 20P2 = 24000000
=> P2 = 1200000Pa
phương trình trạng thái lí tưởng:
\(\dfrac{P_1.V_1}{T_1}=\dfrac{P_2.V_2}{T2}\)
Theo đề bài:
V1 = 120cm3; T1 = 27 + 273 = 300K ; P1 = \(10^5\)Pa
V2 = 20cm3; T2 = 327 + 273 = 600K
Thay vào phương trình:
\(\dfrac{10^5.120}{300}=\dfrac{P_2.20}{600}\Rightarrow P_2=\dfrac{P_1.T_2.V_2}{V_2.T_1}=1200000Pa\)
=12.10^5 Pa