trong mặt phẳng Oxy, cho điểm I (2;-1) và đường thẳng Δ:3x+4y+3=0.Viết phương trình đường tròn tâm I cắt Δ tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB = 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Lời giải:
$I$ là trung điểm $AB$ nên:
\(\left\{\begin{matrix}
\frac{x_A+x_B}{2}=x_I\\
\frac{y_A+y_B}{2}=y_I\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x_B=2x_I-x_A\\
y_B=2y_I-y_A\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x_B=2.0-1=-1\\ y_B=2(-2)-0=-4\end{matrix}\right.\)
Vậy $B(-1,-4)$

HQ
Hà Quang Minh
Giáo viên
29 tháng 9 2023
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
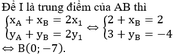

gọi H là trung điểm AB
=> \(IH=d_{\left(I,\Delta\right)}=\dfrac{\left|3\cdot2+4\cdot\left(-1\right)+3\right|}{\sqrt{3^2+4^2}}=1\)
\(S_{\Delta IAB}=2\cdot\left(\dfrac{1}{2}\cdot IH\cdot HA\right)=4\)
\(IH\cdot IA=4\Leftrightarrow1\cdot HA=4\Rightarrow HA=4\)
\(\Rightarrow R=IA=\sqrt{IH^2+HA^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
\(\Rightarrow\) Phương trình đường tròn (x-2)2 +(y+1)2=17