GIÚP MÌNH GIẢI BÀI NÀY VỚI
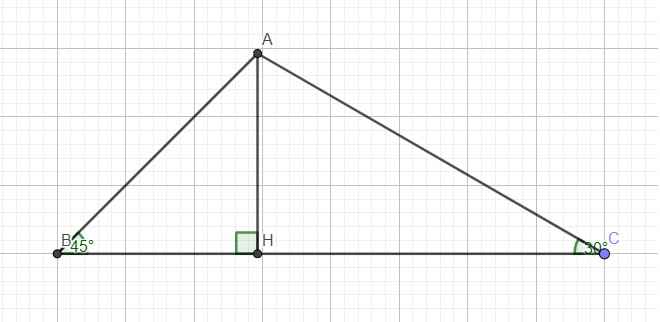
cho tam giác ABC có góc B > góc C. đường cao AH
a) CM: AH <1/2 (AB+AC)
b) Hai đường trung tuyến BM và CN cắt nhau tại G. Trên tia đối của tia MB lấy điểm E sao cho ME=MG. Trên tia đối của tia NC lấy điểm F sao cho NF=NG. CM: EF=BC
c)đường thẳng AG cắt BC tại K. CM : góc AKB > góc AKC