Giải bài toán bài 3 bằng cách lập hệ phương trình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
1
Những câu hỏi liên quan
M
0
5 tháng 5 2020
Đề : Một hình chữ nhật có chu vi bằng 80 cm. Tăng chiều rộng lên 3cm; tăng chiều dài lên 5 cm thì diện tích tăng thêm 195 cm^2.
Tìm chiều dài và chiều rộng ban đầu.
5 tháng 3 2021
Bài 1:
Ta có: \(\left\{{}\begin{matrix}17x+4y=2\\13x+2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}17x+4y=2\\26x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-9x=0\\13x+2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(0;\dfrac{1}{2}\right)\)
5 tháng 3 2021
Bài 2:
Gọi x(km/h) là vận tốc của người thứ nhất(Điều kiện: x>0)
Vận tốc của người thứ hai là: x(km/h)
Quãng đường người thứ nhất đi từ A đến chỗ gặp là: 2x(km)
Quãng đường người thứ hai đi từ B đến chỗ gặp là: 2x(km)
Theo đề, ta có: 2x+2x=180
\(\Leftrightarrow4x=180\)
hay x=45(thỏa ĐK)
Vậy: Vận tốc của hai người là 45km/h
CM
17 tháng 2 2018
Gọi 2 số cần tìm là x; y.
Tổng của 2 số là 59 nên ta có: x + y = 54
Ba lần số này hơn số kia là 2 nên: 3x – y =2
Ta có hệ phương trình:
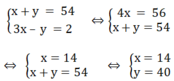
Vậy hai số cần tìm là 14 và 40.
Gọi số tờ tiền loại 200 ngàn đồng là x tờ (x>0)
Số tờ tiền loại 100 ngàn đồng là y tờ (y>0)
Do ba Lan đến được 36 tờ nên: \(x+y=36\)
Do tổng số tiền rút là 6 triệu đồng (\(=6000\) ngàn đồng) nên:
\(200x+100y=6000\Leftrightarrow2x+y=60\)
Ta được hệ: \(\left\{{}\begin{matrix}x+y=36\\2x+y=60\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=24\\y=12\end{matrix}\right.\)