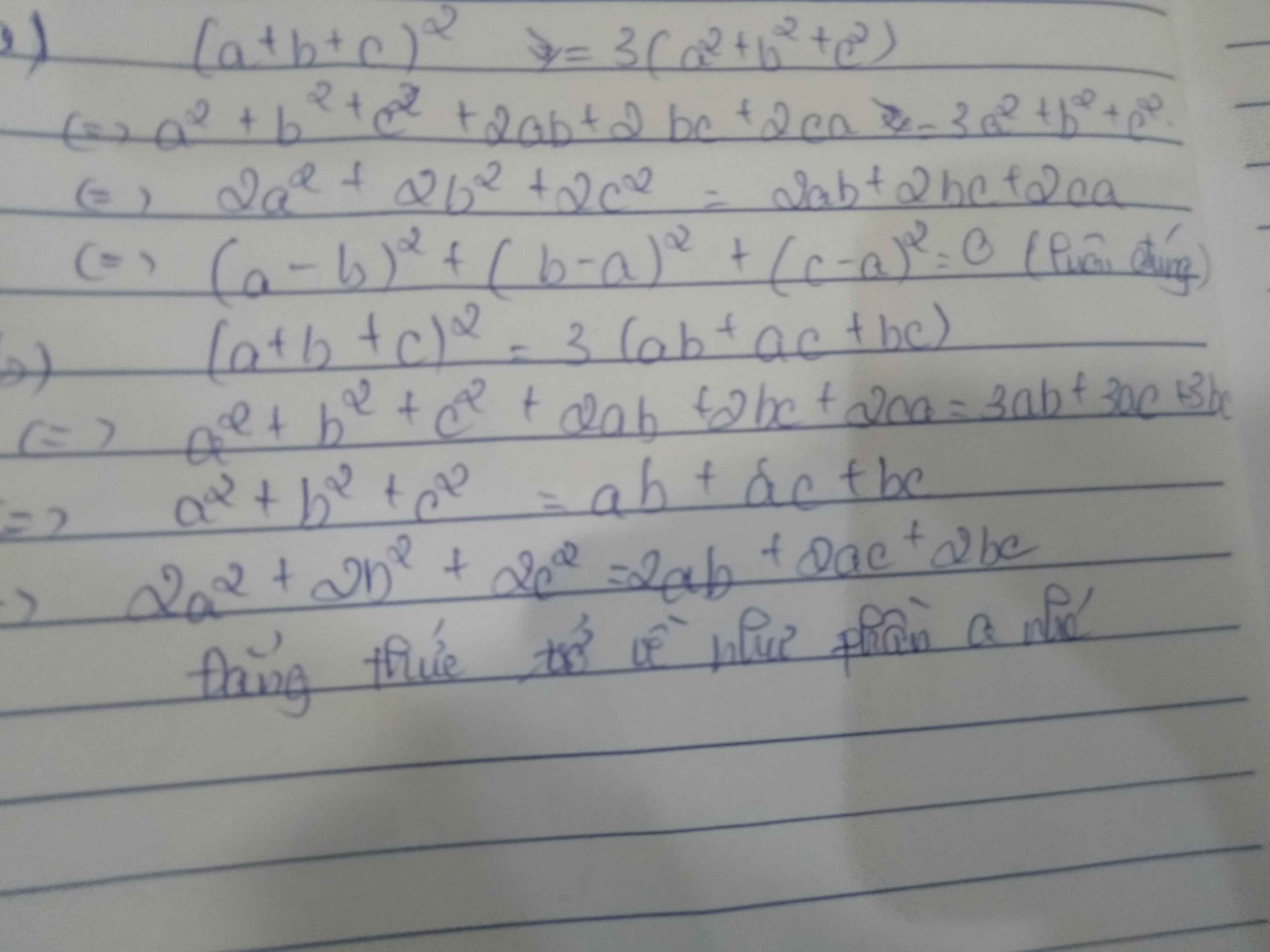cmr aa+b2+c2-ab-ac-bc >= 0 voi moi a, b, c thuoc R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(\left(a+b+c\right)^2=a^2+b^2+c^2\Leftrightarrow ab+bc+ca=0\)
\(\Rightarrow a^3b^3+b^3c^3+c^3a^3=3a^2b^2c^2\)
Ta có:
\(\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}=\dfrac{a^3b^3+b^3c^3+c^3a^3}{a^2b^2c^2}=\dfrac{3a^2b^2c^2}{a^2b^2c^2}=3\)
ML
8 tháng 8 2016
B2: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)=4\)
\(\Rightarrow\orbr{\begin{cases}a+b+c=2\\a+b+c=-2\end{cases}}\)
TH1: \(a+b+c=2\Rightarrow c=2-\left(a+b\right)\)
\(a^2+b^2+c^2=2\)\(\Leftrightarrow a^2+b^2+\left(2-a-b\right)^2=2\)
\(\Leftrightarrow a^2+b^2+ab-2\left(a+b\right)+1=0\)
\(\Leftrightarrow a^2+\left(b-2\right)a+b^2-2b+1=0\)
Xem đây là một phương trình bậc hai ẩn a, tham số b.
Để tồn tại a thỏa phương trình trên thì \(\Delta\ge0\)
\(\Leftrightarrow\left(b-2\right)^2-4\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow b\left(3b-4\right)\le0\)\(\Leftrightarrow0\le b\le\frac{4}{3}\)
Do vai trò của a, b, c là như nhau nên \(0\le a,b,c\le\frac{4}{3}\)
(hoặc đổi biến thành b và tham số a --> CM được a, rồi thay \(b=2-c-a\) sẽ chứng minh được c)
TH2: \(a+b+c=-2\) --> tương tự trường hợp 1 nhưng kết quả sẽ là
\(-\frac{4}{3}\le a,b,c\le0\)
Kết hợp 2 trường hợp lại, ta có đpcm.
TH
2
KT
21 tháng 8 2018
\(ab+bc+ca=0\)
=> \(\frac{ab+bc+ca}{abc}=0\)
=> \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
Đặt: \(\frac{1}{a}=x;\)\(\frac{1}{b}=y;\)\(\frac{1}{c}=z\)
Ta có: \(x+y+z=0\)
=> \(x^3+y^3+z^3=3xyz\) (tự c/m, ko c/m đc ib)
hay \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
\(B=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=abc.\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)
\(=abc.\frac{3}{abc}=3\)
I
0
HN
1
20 tháng 8 2023
Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)
14 tháng 7 2021
`1)(a+b+c)^2=3(a^2+b^2+c^2)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3a^2+3b^2+3c^2`
`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`
`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`
`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`
Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`
Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`
`2)(a+b+c)^2=3(ab+bc+ca)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca`
`<=>a^2+b^2+c^2=ab+bc+ca`
`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`
`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`
`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`
Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`
Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`
Vậy nếu `a=b=c` thì ....
28 tháng 6 2017
a) x2 - 7x + 16
= (x2 - 2x\(\frac{7}{2}\)+ \(\frac{49}{4}\)) + \(\frac{15}{4}\)
= (x - \(\frac{7}{2}\))2 + \(\frac{15}{4}\)> 0
b) 3x2 - 3x + 1
= [\(\left(\sqrt{3x^2}\right)^2\)- 2.\(\sqrt{3x^2}\).\(\frac{\sqrt{3}}{2}\)+ \(\frac{3}{4}\)] + \(\frac{1}{4}\)
= (\(\sqrt{3x^2}\)- \(\frac{\sqrt{3}}{2}\))2 + \(\frac{1}{4}\)> 0
c) -x2 + 3x - 5
= -(x2 - 3x + 5)
= -(x2 - 2x\(\frac{3}{2}\)+ \(\frac{9}{4}\)+\(\frac{11}{4}\))
= -[(x - \(\frac{3}{2}\))2 + \(\frac{11}{4}\)] < 0
d) Câu này sai đề rồi bạn ơi