Một chiếc xe đua đi từ H đến K với vận tốc 64 m/giây. Sau đó đi từ K về H với vận tốc 72 m/giây. Tính quãng đường HK biết thời gian đi từ K về H ít hơn thời gian đi từ H đến K là 2 phút.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi quang duong AB là x (km, x>0)
Thời gian ô tô đi là x/50
Thoi gian o to ve là x/40
Vì t/gian về nhiều hơn t/gian đi là 30 phút(=1/2)nên ta có pt:
x/40-1/2=x/50
đến đây tự giải
đs:100

Ta có: 45 phút =3/4 giờ
Gọi x (km) là chiều dài quãng đường AB (x > 0)
Thời gian đi là: x/12 giờ
Thời gian về là: x/10 giờ
Vì thời gian về nhiều hơn thời gian đi là 3/4 giờ nên ta có phương trình sau:
\(\frac{x}{10}-\frac{x}{12}=\frac{3}{4}\)
Giải phương trình ta được: x = 45 ( TMĐK)
Vậy quãng đường AB có chiều dài là: 45 km
k cho mk nha
Gọi thời gian đi là x (h) ( x>o)
Thời gian về là x+3/4(h)
Quãng đường đi 15x (km)
Quãng đường về 12(x+3/4)(km)
Vì quãng đường AB lúc đi và về không đổi ---> phương trình
15x=12(x+3/4)
---> x=3(tmđk)
--->quãng đường AB dài :15.3=45
Vậy......

Ta có: 24 phút = \(\dfrac{2}{5}giờ\)
Gọi x là quãng đường AB (x>0)
Ta có: thời gian đi là: \(\dfrac{x}{50}\)(km/h)
thời gian về là: \(\dfrac{x}{50+10}=\dfrac{x}{60}\)(km/h)
Ta có: thời gian đi - \(\dfrac{2}{5}=thời\) gian về
\(\dfrac{x}{50}-\dfrac{2}{5}=\dfrac{x}{60}\\ < =>\dfrac{6x}{300}-\dfrac{120}{300}=\dfrac{5x}{300}\\ < =>6x-120=5x\\ < =>6x-5x=120\\ < =>x=120\left(km\right)\)
Vậy quãng đường AB dài 120km
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Thời gian người đó đi từ A đến B là:
\(\dfrac{x}{50}\left(h\right)\)
Thời gian người đó đi từ B về A là:
\(\dfrac{x}{50+10}=\dfrac{x}{60}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{50}-\dfrac{x}{60}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{6x}{300}-\dfrac{5x}{300}=\dfrac{120}{300}\)
Suy ra: 6x-5x=120
hay x=120(thỏa ĐK)
Vậy: AB=120km

Vận tốc lúc về: \(35+7=42\) (km/h)
Gọi thời gian về là x>0 (giờ) \(\Rightarrow\) thời gian đi là \(x+\dfrac{1}{2}\) giờ
Quãng đường lúc đi: \(35\left(x+\dfrac{1}{2}\right)\) (km)
Quãng đường lúc về: \(42x\) (km)
Do quãng đường đi và về bằng nhau nên ta có pt:
\(35\left(x+\dfrac{1}{2}\right)=42x\)
\(\Leftrightarrow7x=\dfrac{35}{2}\Rightarrow x=\dfrac{5}{2}\) (giờ)
Độ dài quãng đường: \(S=42.\dfrac{5}{2}=105\) (km)

Gọi độ dài quãng đường AB là x (km), (x > 0, km)
Thời gian đi từ A đến B: 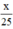 (giờ)
(giờ)
Thời gian đi từ B đến A: 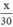 (giờ)
(giờ)
Thời gian về ít hơn thời gian đi 20 phút = 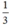 giờ nên ta có phương trình:
giờ nên ta có phương trình:
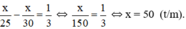
Vậy quãng đường AB dài 50km.

Gọi \(x\) với đơn vị là \(km\) là độ dài quãng đường \(AB\left(x>0\right)\).
Thời gian đi của người đó là : \(\dfrac{x}{25}\left(h\right)\)
Thời gian về của người đó là :\(\dfrac{x}{30}\left(h\right)\).
Do thời gian về ít hơn thời gian đi là \(20\left(phút\right)=\dfrac{1}{3}\left(h\right)\) nên ta có phương trình :
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\) \(\Leftrightarrow\dfrac{x}{150}=\dfrac{1}{3}\Leftrightarrow x=50\) (thỏa mãn).
Vậy : Quãng đường AB dài 50km.
Gọi độ dài quãng đường `AB` là : `x(x>0;km)`
Thời gian ô tô đi từ `A` đến `B` là : `x/25 (h)`
Thời gian ô tô đi từ `B` đến `A` là : `x/30 (h)`
Đổi `20` phút `=20/60 =1/3 (h)`
Theo bài ra ta có phương trình :
`x/25 - x/30 =1/3`
`<=> (6x)/150 - (5x)/150 =50/150`
`<=> 6x-5x=50`
`<=>x=50`
Vậy độ dãi quãng đường `AB` là `50km`