Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bạn tách ra nhá
Thôi, mình làm câu 1:
Vì thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch
V xuôi/V ngược = T ngược/T xuôi = 40/30 = 4/3
Ta có sơ đồ:
T xuôi: |-----|-----|-----| 30 phút
T ngược:|-----|-----|-----|-----|
T xuôi là:
30 : (4 - 3) x 3 = 90 phút = 1,5 giờ
Quãng đường là:
1,5 x 40 = 60km
Đ/s:..
Vì quãng đường AB không đổi nên ta có :Đổi: \(45ph=\dfrac{3}{4}h\)
Gọi thời gian người đó đi từ A đến B là x (h) (x > 0)
Thời gian người đó từ B về A là
\(x-\dfrac{3}{4}\left(h\right)\)
Quãng đường người đó đi từ A đến B là 30x (km)
Quãng đường người đó đi từ A đến B là:
\(40.\left(x-\dfrac{3}{4}\right)=40x-30\left(km\right)\)
Vì quãng đường AB không đổi nên ta có :\(40x-30=30x\Leftrightarrow10x=30\Leftrightarrow x=3\left(h\right)\)Độ dài quãng đường AB là:
\(30.3=90\left(km\right)\)
Đổi 30 phút = \(\dfrac{1}{2}\) (giờ)
Gọi x (km) là quãng đường từ A đến B (ĐK : x > 0)
Thời gian đi : \(\dfrac{x}{30}\left(h\right)\)
Thời gian về : \(\dfrac{x}{40}\left(h\right)\)
Vì thời gian về ít hơn thời gian đi 30 phút nên ta có pt:
\(\dfrac{x}{40}+\dfrac{x}{30}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{3x}{120}+\dfrac{4x}{120}=\dfrac{60}{120}\)
\(\Leftrightarrow7x=60\)
\(\Leftrightarrow x=\dfrac{60}{7}\) (N)
Vậy : quãng đường AB dài \(\dfrac{60}{7}\left(km\right)\)
\(45\)phút \(=\)\(\frac{3}{4}\)giờ
Gọi quãng đường AB là: \(a\)km (a > 0)
Thời gian đi là: \(\frac{a}{40}\)giờ
Thời gian về là: \(\frac{a}{30}\)giờ
Ta có phương trình \(\frac{a}{30}-\frac{a}{40}=\frac{3}{4}\)
\(\Leftrightarrow\)\(\frac{4a}{120}-\frac{3a}{120}=\frac{3}{4}\)
\(\Leftrightarrow\)\(\frac{a}{120}=\frac{3}{4}\)
\(\Leftrightarrow\) \(a=\frac{120.3}{4}=90\)
Vậy quãng đường AB dài \(90\)km
đổi 45p = \(\dfrac{3}{4}h\)
gọi quãng đường AB là x(km)(x>0)
có
\(V_{\text{đ}i}=40\left(\text{km/h}\right)\\
V_{v\text{ề}}=30\left(\text{km/h}\right)\\
t_{\text{đ}i}=\dfrac{x}{40}\left(h\right)\\
t_{v\text{ề}}=\dfrac{x}{30}\left(h\right)\)
theo bài ra ta có pt
\(\dfrac{x}{30}-\dfrac{x}{40}=\dfrac{3}{4}\\
\Leftrightarrow\dfrac{4x}{120}-\dfrac{3x}{120}=\dfrac{90}{120}\\
\Leftrightarrow4x-3x=90\\
\Leftrightarrow x=90\left(t\text{m}\right)\)
=> qđ AB dài 90km
Gọi độ dài quãng đường AB là x (km), (x > 0, km)
Thời gian đi từ A đến B: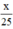 
(giờ)
Thời gian đi từ B đến A: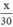 
(giờ)
Thời gian về ít hơn thời gian đi 20 phút =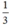 
giờ nên ta có phương trình:
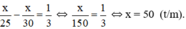
Vậy quãng đường AB dài 50km.
Gọi \(x\) với đơn vị là \(km\) là độ dài quãng đường \(AB\left(x>0\right)\).
Thời gian đi của người đó là : \(\dfrac{x}{25}\left(h\right)\)
Thời gian về của người đó là :\(\dfrac{x}{30}\left(h\right)\).
Do thời gian về ít hơn thời gian đi là \(20\left(phút\right)=\dfrac{1}{3}\left(h\right)\) nên ta có phương trình :
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\) \(\Leftrightarrow\dfrac{x}{150}=\dfrac{1}{3}\Leftrightarrow x=50\) (thỏa mãn).
Vậy : Quãng đường AB dài 50km.
Gọi độ dài quãng đường `AB` là : `x(x>0;km)`
Thời gian ô tô đi từ `A` đến `B` là : `x/25 (h)`
Thời gian ô tô đi từ `B` đến `A` là : `x/30 (h)`
Đổi `20` phút `=20/60 =1/3 (h)`
Theo bài ra ta có phương trình :
`x/25 - x/30 =1/3`
`<=> (6x)/150 - (5x)/150 =50/150`
`<=> 6x-5x=50`
`<=>x=50`
Vậy độ dãi quãng đường `AB` là `50km`
Gọi a là thời gian lúc đi của người đó (h) (a>0)
Đổi 45p=0,75h
Quãng đường lúc đi là 40a (km); Quãng đường khi về là 30(a+0,75) (h)
Vì cùng là quãng đường AB nên ta có:
40a= 30(a+0,75)
<=> 40a - 30a = 22,5
<=> 10a = 22,5
<=>a= 2,25(TM)
Vậy quãng đường AB dài: 40a= 40.2,25=90(km)