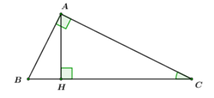
cho tam giác abc góc a bằng 90 độ , đường cao AH, cho AC = 4cm, AB = 3cm. Tính AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm

Có ai biết làm bài này ko,,,mình cũng đag mắc bài này nè

3:
Đặt HB=x; HC=y
Theo đề, ta có: x+y=289 và xy=120^2=14400
=>x,y là các nghiệm của phương trình:
a^2-289a+14400=0
=>a=225 hoặc a=64
=>(x,y)=(225;64) và (x,y)=(64;225)
TH1: BH=225cm; CH=64cm
=>\(AB=\sqrt{225\cdot289}=15\cdot17=255\left(cm\right)\) và \(AC=\sqrt{64\cdot289}=7\cdot17=119\left(cm\right)\)
TH2: BH=64cm; CH=225cm
=>AB=119m; AC=255cm

a: BH=0,5dm=5cm
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>AH^2=13^2-5^2=12^2
=>AH=12cm
sin B=AH/AB=12/13
sin C=sin HAC=BH/AB=5/13
b: ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>AH=2*căn 3(cm)
BC=3+4=7cm
\(AB=\sqrt{BH\cdot BC}=\sqrt{21}\left(cm\right)\)
\(AC=\sqrt{4\cdot7}=2\sqrt{7}\left(cm\right)\)
Xét ΔABC vuông tại A có
sin C=AB/BC=căn 21/7
sin B=AC/BC=2/căn 7

Tham khảo tại đây nha:
https://hoc24.vn/hoi-dap/question/887221.html

Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B

a, Xét Δ ABC, có :
\(AB^2+AC^2=BC^2\) (định lí Py - ta - go)
=> \(3^2+4^2=BC^2\)
=> \(25=BC^2\)
=> BC = 5 (cm)
Xét Δ ABC vuông tại A, theo hệ thức lượng có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
=> \(\dfrac{1}{AH^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}\)
=> AH = 2,4 cm
b, Xét Δ ABD, có :
HD = HB (gt)
AH là đường cao
=> Δ ABD cân
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{3^2+4^2}\\ \Rightarrow BC=5\left(cm\right)\)
Ta có: \(S_{ABC}=\dfrac{AB.AC}{2}\)
Ta lại có: \(S_{ABC}=\dfrac{AH.BC}{2}\)
\(\Rightarrow\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\\ \Rightarrow AB.AC=AH.BC\\ \Rightarrow3.4=5.AH\\ \Rightarrow AH=\dfrac{12}{5}\left(cm\right)\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}cm\)
e tự trình bày ra