tìm số nguyên x , y thỏa mãn sao cho ;
xy + 2x + y + 11 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)

xy+x-y=4
=>(xy+x)-(y+1)=3
=>(y+1)(x-1)=3
Mà x;y nguyên nên (x-1);(y+1) thuộc Ư(3)={1;-1;3;-3}
Đến đây bạn lập bảng là ra
xy+x-y=4
=>(xy+x)-(y+1)=3
=>(y+1)(x-1)=3
Mà x;y nguyên nên (x-1);(y+1) thuộc Ư(3)={1;-1;3;-3}
Đến đây bạn lập bảng là ra

Chọn C.
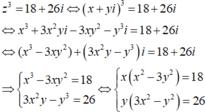
Do x; y nguyên nên
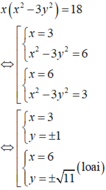
Mà y(3x2 – y2 ) = 26 ⇒ x = 3; y = 1.

ta thấy 2=0+2=2+0=1+1
Trường hợp 1:
Với lxI =0 thì x=0
lyl =2 thì y=-2 hoặc 2
=> với trường hợp 1 thì có 2 cặp (x,y) thỏa mãn là x=0;y=-2 và x=0;y=2.
Trường hợp 2:
Với lxl =2 thì x=-2 hoặc 2
lyl =0 thì y=0
=>với trường hợp 2 thì có 2 cặp (x,y) thỏa mãn là x=-2;y=0 và x=2;y=0.
Trường hợp 3:
Với lxl =1 thì x=-1 hoặc 1
lyl =1 thì y=-1 hoặc 1
=>với trường hợp 3 thì có 4 cặp (x,y) thỏa mãn là x=-1;y=-1
x=-1;y=1
x=1;y=-1
x=1;y=1
Vậy qua 3 trường hợp thì có thì có 4+2+2=8 cặp (x,y) thỏa mãn yêu cầu đề bài.
ta thấy 2=0+2=2+0=1+1
Trường hợp 1:
Với lxI =0 thì x=0
lyl =2 thì y=-2 hoặc 2
=> với trường hợp 1 thì có 2 cặp (x,y) thỏa mãn là x=0;y=-2 và x=0;y=2.
Trường hợp 2:
Với lxl =2 thì x=-2 hoặc 2
lyl =0 thì y=0
=>với trường hợp 2 thì có 2 cặp (x,y) thỏa mãn là x=-2;y=0 và x=2;y=0.
Trường hợp 3:
Với lxl =1 thì x=-1 hoặc 1
lyl =1 thì y=-1 hoặc 1
=>với trường hợp 3 thì có 4 cặp (x,y) thỏa mãn là x=-1;y=-1
x=-1;y=1
x=1;y=-1
x=1;y=1
Vậy qua 3 trường hợp thì có thì có 4+2+2=8 cặp (x,y) thỏa mãn yêu cầu đề bài.

xy + 2x + y + 11 = 0
=>x(y+2)+y+11=0
=>x(y+2)+(y+2)+9=0
=>(y+2)(x+1)+9=0
=>(y+2)(x+1)=0-9
=>(y+2)(x+1)=-9
Mà x;y là số nguyên
=>y+2 và x+1 là các ước của 9
Mà Ư(9)={1;-1;3;-3;9;-9}
Ta có bảng sau
(x;y) cần tìm là (0;7) ; (-2;-11) ; (2;1) ;(-4;-5) ; (8;-1) ; (-10;-3)
nhầm các kết quả là đối dấu với kết quả trên