Bài 1: Tam giác ABC và tam giác MNP đồng dạng, Biết
BC= 10; AC= 12. Tính số đo các góc C, M, N, P và độ dài cạnh NP.
Bài 2: Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD
= 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chứng minh rằng:
a) Δ AED ω ΔΑBC
b) ABE = ACD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔABC~ΔKHG
=>\(\dfrac{AB}{KH}=\dfrac{2}{3}\)
=>\(KH=AB\cdot\dfrac{3}{2}\)
ΔKHG~ΔMNP
=>\(\dfrac{KH}{MN}=\dfrac{1}{3}\)
=>\(\dfrac{AB}{MN}\cdot\dfrac{3}{2}=\dfrac{1}{3}\)
=>\(\dfrac{AB}{MN}=\dfrac{1}{3}:\dfrac{3}{2}=\dfrac{2}{9}\)
=>ΔABC đồng dạng với ΔMNP theo tỉ số \(\dfrac{2}{9}\)

Câu 1 : Nếu 2 tam giác vuông có 2 góc nhọn tương ứng bằng nhau thì chúng được gọi là đồng dạng với nhau vì đương nhiên trừ góc vuông ở cả hai tam giác vuông thì góc nhọn còn lại đương nhiên phải bằng nhau.
Câu 2 : Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng. Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng.

![]()
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
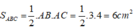
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
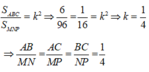
Thay số
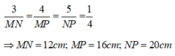
Chọn đáp án B
Bài 2:
a: AE=AC-CE=16-13=3(cm)
AD=AB-BD=8-2=6(cm)
Xét ΔAED và ΔABC có
AE/AB=AD/AC
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔABC
b: Ta có: ΔAED∼ΔABC
nên AE/AB=AD/AC
hay AB/AC=AE/AD
Xét ΔABE và ΔACD có
AB/AC=AE/AD
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACD
Suy ra: \(\widehat{ABE}=\widehat{ACD}\)