Cho phương trình x2 - (m + 5)x - m + 6 = 0 (1)
a) Giải phương trình với m = 1
b) Tìm các giá trị của m để phương trình (1) có một nghiệm x = - 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2021
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
CM
10 tháng 8 2018
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0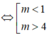 
Do x1 < x2 < 1
30 tháng 3 2022
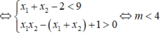
a: Khi m=-1 thì pt sẽ là \(x^2-\left(-1+2\right)x-\left(-1\right)-3=0\)
\(\Leftrightarrow x^2-x-2=0\)
=>x=2 hoặc x=-1
b: \(\Delta=\left(m+2\right)^2-4\left(-m-3\right)\)
\(=m^2+4m+4+4m+12\)
\(=m^2+8m+16=\left(m+4\right)^2\)
=>Phương trình luôn có hai nghiệm
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2>1\)
\(\Leftrightarrow\left(m+2\right)^2-2\left(-m-3\right)>1\)
\(\Leftrightarrow m^2+4m+4+2m+6-1>0\)
\(\Leftrightarrow\left(m+3\right)^2>0\)
=>m<>-3
CM
23 tháng 10 2019
a. + Với m = − 1 2 phương trình (1) trở thành x 2 − 4 x = 0 ⇔ x = 0 x = 4 .
+ Vậy khi m = − 1 2 phương trình có hai nghiệm x= 0 và x= 4.
b. + Phương trình có hai nghiệm dương phân biệt khi
Δ = 2 m + 5 2 − 4 2 m + 1 > 0 x 1 + x 2 = 2 m + 5 > 0 x 1 . x 2 = 2 m + 1 > 0
+ Ta có Δ = 2 m + 5 2 − 4 2 m + 1 = 4 m 2 + 12 m + 21 = 2 m + 3 2 + 12 > 0 , ∀ m ∈ R
+ Giải được điều kiện m > − 1 2 (*).
+ Do P>0 nên P đạt nhỏ nhất khi P 2 nhỏ nhất.
+ Ta có P 2 = x 1 + x 2 − 2 x 1 x 2 = 2 m + 5 − 2 2 m + 1 = 2 m + 1 − 1 2 + 3 ≥ 3 ( ∀ m > − 1 2 ) ⇒ P ≥ 3 ( ∀ m > − 1 2 ) .
và P = 3 khi m= 0 (thoả mãn (*)).
+ Vậy giá trị nhỏ nhất P = 3 khi m= 0.
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
a. Bạn tự giải
b.
\(\Delta=\left(3m-1\right)^2-4\left(2m^2+2m\right)=m^2-14m+1\)
Pt có 2 nghiệm pb khi \(m^2-14m+1>0\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3m-1\\x_1x_2=2m^2+2m\end{matrix}\right.\)
\(\left|x_1-x_2\right|=2\Leftrightarrow\left(x_1-x_2\right)^2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4\)
\(\Leftrightarrow\left(3m-1\right)^2-4\left(2m^2+2m\right)=4\)
\(\Leftrightarrow m^2-14m-3=0\Rightarrow m=7\pm2\sqrt{13}\) (đều thỏa mãn (1))
Lời giải:
a. Với $m=1$ thì pt trở thành:
$x^2-6x+5=0$
$\Leftrightarrow (x-1)(x-5)=0$
$\Leftrightarrow x-1=0$ hoặc $x-5=0$
$\Leftrightarrow x=1$ hoặc $x=5$
b.
Để pt có nghiệm $x=-2$ thì:
$(-2)^2-(m+5)(-2)-m+6=0$
$\Leftrightarrow 4+2(m+5)-m+6=0$
$\Leftrightarrow 20+m=0$
$\Leftrightarrow m=-20$