Hai tiếp tuyến tại B và C của (O) cắt nhau tại A. Lấy điểm M thuộc dây BC sao cho MB<MC. Đường thẳng vuông góc với OM tại M cắt AB ở I, cắt đường thẳng AC ở K. Chứng minh:
a) Hai tứ giác OMIB và OMCK nội tiếp
b) M là trung điểm của IK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

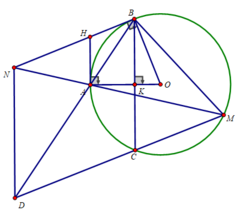
b) Ta có: Một phần đường kính OA vuông góc dây BC
⇒ AB = AC ⇒ sđ cung AB = sđ cung AC
⇒ ∠(BAH) = ∠(ABC) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn 2 cung bằng nhau)
Tứ giác ABMC nội tiếp (O)
⇒ ∠(NMC) = ∠(ABC) (2 góc nội tiếp cùng chắn cung AC)
Do đó: ∠(NMC) = ∠(BAH)

a: góc OBI+góc OMI=180 độ
=>OBIM nội tiếp
góc OMK+góc OCK=180 độ
=>OCKM nội tiếp
b; OBIM nội tiếp
=>góc OIM=góc OBM
OMCK nội tiếp
=>góc OKM=góc OCM
mà góc OBM=góc OCM
nên góc OIM=góc OKM
=>ΔOIK cân tại O
mà OM là đường cao
nên M là trung điểm của IK

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔCAB vuông tại C có CM là đường cao
nên \(CB^2=BM\cdot BA\)
=>\(CB=\sqrt{1\cdot6}=\sqrt{6}\left(cm\right)\)
b: ΔOAC cân tại O
mà OE là đường cao
nên OE là phân giác của \(\widehat{AOC}\)
Xét ΔOAE và ΔOCE có
OA=OC
\(\widehat{AOE}=\widehat{COE}\)
OE chung
Do đó: ΔOAE=ΔOCE
=>\(\widehat{OCE}=\widehat{OAE}=90^0\)
=>EC là tiếp tuyến của (O)

5:
a: góc OAM+góc OBM=180 độ
=>OAMB nội tiếp
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB
b: góc DEB=1/2*sđ cung DB=90 độ
=>BE vuông góc DM
ΔDBM vuông tại B có BE là đường cao
nên MB^2=ME*MD
giúp em với ạ