Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

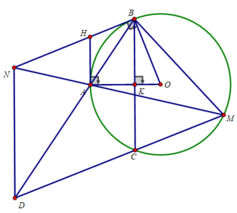
c) 2 tiếp tuyến HA và HB cắt nhau tại H
⇒ ΔHAB cân tại H ⇒ ∠(BAH) = ∠(HBA)
Theo ý b) ∠(NMC) = ∠(BAH)
⇒ ∠(NMC) = ∠(HBA)
Xét tứ giác MBND có: ∠(NMC) = ∠(HBA)
⇒ 2 đỉnh M và B cùng nhìn cạnh ND dưới 1 góc bằng nhau
⇒ MBND là tứ giác nội tiếp.c) 2 tiếp tuyến HA và HB cắt nhau tại H
⇒ ΔHAB cân tại H ⇒ ∠(BAH) = ∠(HBA)
Theo ý b) ∠(NMC) = ∠(BAH)
⇒ ∠(NMC) = ∠(HBA)
Xét tứ giác MBND có: ∠(NMC) = ∠(HBA)
⇒ 2 đỉnh M và B cùng nhìn cạnh ND dưới 1 góc bằng nhau
⇒ MBND là tứ giác nội tiếp.

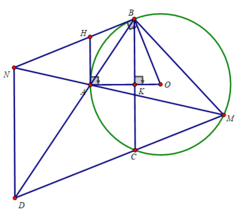
d) Xét tứ giác MBND nội tiếp có:
∠(BDN) = ∠(BMN) (2 góc nội tiếp cùng chắn cung BN)
Xét tứ giác ABMC nội tiếp (O) có:
∠(ABC) = ∠(BMN) (2 góc nội tiếp cùng chắn cung bằng nhau )
⇒ ∠(BDN) = ∠(ABC)
Mà 2 góc này ở vị trí so le trong
⇒ ND // BC
Mà BC ⊥ OA ⇒ ND ⊥ OA

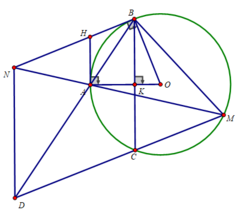
a) Xét tứ giác OBHA có:
∠(OBH) = 90 0 ( BH là tiếp tuyến của (O)
∠(OAH) = 90 0 (AH là tiếp tuyến của (O)
⇒ ∠(OBH) + ∠(OAH) = 180 0
⇒ Tứ giác OBHA là tứ giác nội tiếp

\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)

a: Xét ΔOBM vuông tại B có BI là đường cao
nên \(OI\cdot OM=OB^2\)
=>\(OM\cdot2=5^2=25\)
=>OM=25/2=12,5(cm)
Ta có: ΔBIO vuông tại I
=>\(IB^2+IO^2=BO^2\)
=>\(IB^2+2^2=5^2\)
=>\(IB^2=21\)
=>\(IB=\sqrt{21}\left(cm\right)\)
Ta có: ΔOBC cân tại O
mà OI là đường cao
nên I là trung điểm của BC và OI là phân giác của góc BOC
Ta có: I là trung điểm của BC
=>\(BC=2\cdot BI=2\sqrt{21}\left(cm\right)\)
c: Xét ΔOBM và ΔOCM có
OB=OC
\(\widehat{BOM}=\widehat{COM}\)
OM chung
Do đó: ΔOBM=ΔOCM
=>\(\widehat{OBM}=\widehat{OCM}=90^0\)
=>MC là tiếp tuyến của (O)

a.Xét 2 tam giác vuông ABO và ACO có
BO=CO (đều là BK đường tròn)
AB=AC (Độ dài hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm bên ngoài đường tròn thì bằng nhau)
góc ABO=góc ACO=90 độ
Suy ra tam giác ABO=tam giác ACo (c.g.c) suy ra góc BAO=góc CAO
Tam giác ABC cân tại A nên AO vừa là phân giác của góc BAC vừa là đường cao của tam giác ABC hạ từ A xuống BC vậy AO vuông góc với BC
c,Ta có góc BCO=góc CAO (cùng phụ với góc AOC)
góc CAO=góc BAO
suy ra góc BCO=góc BAO (1)
Xét tam giác vuông BCH có góc CBH+góc BCO=90 độ (2)
Ta có góc ABC+góc BAO=90 độ (3)
Từ (1) (2) (3) suy ra góc CBH=góc ABC nên BC là phân giác của góc ABH
mình chỉ biết làm câu a và c thôi mong bạn thông cảm

c: Xét (O) có
ΔMKD nội tiếp
MD là đường kính
Do đó: ΔMKD vuông tại K
=>MK\(\perp\)KD tại K
=>MK\(\perp\)AD tại K
Xét ΔMDA vuông tại M có MK là đường cao
nên \(AK\cdot AD=AM^2\left(1\right)\)
Xét ΔAOM vuông tại M có MH là đường cao
nên \(AH\cdot AO=AM^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AD=AH\cdot AO\)
b) Ta có: Một phần đường kính OA vuông góc dây BC
⇒ AB = AC ⇒ sđ cung AB = sđ cung AC
⇒ ∠(BAH) = ∠(ABC) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn 2 cung bằng nhau)
Tứ giác ABMC nội tiếp (O)
⇒ ∠(NMC) = ∠(ABC) (2 góc nội tiếp cùng chắn cung AC)
Do đó: ∠(NMC) = ∠(BAH)