xin nhờ các cao nhân giải bài này giúp e với ạ. e thành tâm cảm ơn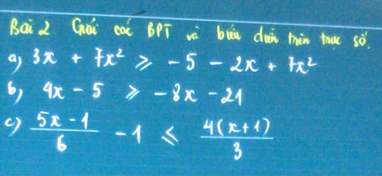
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 1.
a.Áp dụng tính chất đường phân giác, ta có:
\(\dfrac{AB}{AH}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{CH}{8}=\dfrac{BC}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{CH+BC}{8+6}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(CH=\dfrac{5}{7}.8=\dfrac{40}{7}\)
\(BC=\dfrac{5}{7}.6=\dfrac{30}{7}\)
b.\(\Delta ABH\) là tam giác vuông vì:
\(HB^2=AB^2+AH^2\)
\(\Leftrightarrow10^2=6^2+8^2\) ( pitago đảo )
Áp dụng định lý pitago vào tam giác vuông ACB
\(AB^2=BC^2+AC^2\)
\(\Rightarrow AC=\sqrt{6^2-\dfrac{30}{7}^2}=\dfrac{12\sqrt{6}}{7}\)
\(S_{ABC}=\dfrac{1}{2}.BC.AC=\dfrac{1}{2}.\dfrac{30}{7}.\dfrac{12\sqrt{6}}{7}\simeq8,998cm^2\)
\(S_{ACH}=\dfrac{1}{2}.HC.AC=\dfrac{1}{2}.\dfrac{40}{7}.\dfrac{12\sqrt{6}}{7}\simeq11,997cm^2\)

Xét ΔABC có BD là phân giác
nên AB/AD=BC/CD
=>AB/4=BC/5
Đặt AB/4=BC/5=k
=>AB=4k; BC=5k
Theo đề, ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow9k^2=81\)
=>k=3
=>AB=12; BC=15
Vì BD là phân giác của \(\widehat{ABC}\) nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\Leftrightarrow\dfrac{4}{AB}=\dfrac{5}{BC}\Leftrightarrow BC=\dfrac{5AB}{4}\)
Có : AC=AD+DC=4+5=9cm
Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) ( định lí Pi-ta-go)
\(AB^2+81=\dfrac{25AB^2}{16}\)
\(81=\dfrac{25AB^2}{16}-\dfrac{16AB^2}{16}\)
\(\Leftrightarrow\dfrac{9AB^2}{16}=81\)
\(9AB^2=1296\)
\(AB^2=144\)
AB=12 cm
Có : \(BC=\dfrac{5AB}{4}=\dfrac{5.12}{4}=15cm\)

a:Xét ΔAMN có MB là tia phân giác
nên AB/BN=AM/MN=AN/MN(1)
Xét ΔAMN có NC là tia phân giác
nên AC/CM=AN/MN(2)
Từ (1) và (2) suy ra AB/BN=AC/CM
hay BC//MN
b: Xét ΔCBM có \(\widehat{CBM}=\widehat{CMB}\)
nên ΔCBM cân tại C
=>CB=CM=6cm
Xét ΔABC có BC//MN
nên BC/MN=AC/AM
\(\Leftrightarrow\dfrac{AC}{AC+6}=\dfrac{1}{2}\)
=>AC=6(cm)
=>AM=12(cm)

\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)


1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn

Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8

\(c2:3x+5x^2\ge-6+5x+5x^2\Leftrightarrow2x-6\le0\Leftrightarrow x\le3\)
\(c3:-x+7=6a-1\Leftrightarrow x=-\left(6a-1-7\right)=8-6a>0\Leftrightarrow a< \dfrac{4}{3}\)
\(c4:pt\Leftrightarrow\left(2019-x\right)^3+\left(2021-x\right)^3+\left[2x-4040\right]^3=0\left(1\right)\)
\(đặt:\left[\left(2019-x\right);\left(2021-x\right)\right]=\left\{u;v\right\}\)
\(\Rightarrow2x-4040=x-2019+x-2021=-u-v\)
\(\left(1\right)\Leftrightarrow u^3+v^3+\left(-u-v\right)^3=0\Leftrightarrow-3uv\left(u+v\right)=0\Leftrightarrow\left[{}\begin{matrix}u.v=0\\u=-v\end{matrix}\right.\)
\(u.v=0\Leftrightarrow\left[{}\begin{matrix}u=0\Leftrightarrow2019-x=0\Leftrightarrow x=2019\\v=0\Leftrightarrow2021-x=0\Leftrightarrow x=2021\end{matrix}\right.\)
\(u=-v\Leftrightarrow2019-x=x-2021\Leftrightarrow x=2020\)
\(\Rightarrow S=\left\{2019;2020;2021\right\}\)
Câu 2 :
\(\Leftrightarrow3x+5x^2+6-5x-5x^2\ge0\Leftrightarrow-2x+6\ge0\Leftrightarrow x\le3\)
Câu 4 :
PT <=> \(2019-x+2021-x+2x-4040=0\Leftrightarrow2019+2021-4040=0\)
( đúng )
Vậy pt có vô số nghiệm






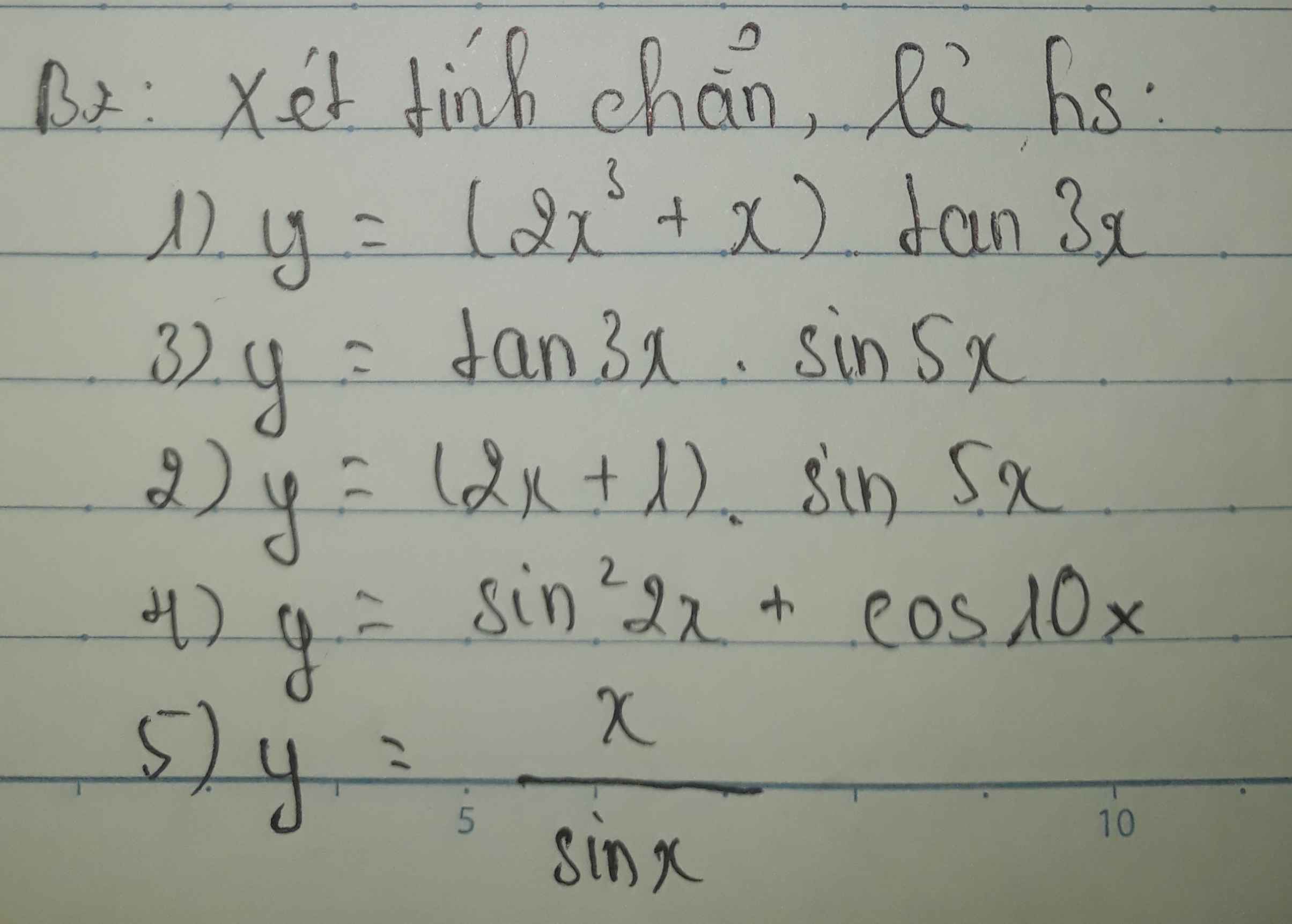


a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)