Một xe máy đi từ A đến B với vận tốc 40km/h đến B nghỉ 30 phút. Sau đó quay về A với vận tốc là 30km/h. Biết thời gian đi và về là 6h30. Tính quãng đường AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi quãng đường AB là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{x}{30}+\dfrac{1}{2}+\dfrac{x}{40}=5+\dfrac{1}{6}\Rightarrow x=80\left(tm\right)\)

Đổi: 3 giờ 40 phút = \(\dfrac{11}{3}\) giờ; 10 phút = \(\dfrac{1}{6}\) giờ
Gọi độ dài quãng đường AB là x (km)
(ĐK: x > 0)
Thời gian xe máy đi từ A đến B là: \(\dfrac{x}{40}\) (giờ)
Thời gian xe máy đi từ B về A là: \(\dfrac{x}{30}\) (giờ)
Mà thời gian tổng cộng hết 11/3 giờ nên ta có pt:
\(\dfrac{x}{40}+\dfrac{1}{6}+\dfrac{x}{30}=\dfrac{11}{3}\\ \Leftrightarrow\dfrac{3x}{120}+\dfrac{20}{120}+\dfrac{4x}{120}=\dfrac{440}{120}\\ \Leftrightarrow3x+4x+20=440\\ \Leftrightarrow7x=420\\ \Leftrightarrow x=60\left(tmđk\right)\)
Vậy quãng đường AB dài 60km
Đổi \(3h40'=\dfrac{11}{3}h\)
\(10'=\dfrac{1}{6}h\)
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Thời gian xe máy đi từ A đến B là:
\(\dfrac{x}{40}\left(h\right)\)
Thời gian xe máy đi từ B về A là:
\(\dfrac{x}{30}\left(h\right)\)
Theo đề, ta có: \(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{6}=\dfrac{11}{3}\)
\(\Leftrightarrow\dfrac{3x}{120}+\dfrac{4x}{120}=\dfrac{11}{3}-\dfrac{1}{6}=\dfrac{21}{6}\)
\(\Leftrightarrow\dfrac{7x}{120}=\dfrac{7}{2}\)
\(\Leftrightarrow7x=420\)
hay x=60(thỏa ĐK)
Vậy: Độ dài quãng đường AB là 60km

10 phút = \(\dfrac{1}{6}\) giờ
6 giờ 40 phút = \(\dfrac{20}{3}\) (giờ)
Gọi x (km) là độ dài quãng đường AB (Điều kiện: x ∈ Z; x > 0)
Thời gian đi từ A đến B là \(\dfrac{x}{30}\) (giờ)
Thời gian đi từ B đến A là \(\dfrac{x}{35}\) (giờ)
Theo đề bài ta có phương trình:
\(\dfrac{x}{30}+\dfrac{x}{35}+\dfrac{1}{6}\) = \(\dfrac{20}{3}\)
MSC (mẫu số chung): 1050
Quy đồng mẫu hai vế và khử mẫu ta được:
35x + 30x + 175 = 7000
⇔ 35x + 30x = 7000 - 175
⇔ 65x = 6825
⇔ x = 105 (nhận)
Vậy quãng đường AB dài 105 km

Gọi độ dài AB là x
Theo đề, ta có: x/30+x/25+1/6=5+2/3
=>x=75
Lời giải:
Thời gian đi lần về (không tính thời gian nghỉ) là:
$5h40'-10'=5h30'=5,5h$
Thời gian đi: $\frac{AB}{30}$ (h)
Thời gian về: $\frac{AB}{25}$ (h)
Tổng thời gian đi và về: $\frac{AB}{30}+\frac{AB}{25}=5,5$
$\Leftrightarrow AB.\frac{11}{150}=5,5$
$\Rightarrow AB=75$ (km)

9h15p=9,25h
30p=0,5h
Gọi quãng đường AB là x (km) đk: x>0
Thời gian xe đi từ A đến B: \(\dfrac{x}{40}\)(h)
Thời gian xe đi từ B về A: \(\dfrac{x}{30}\)(h)
Theo bài, ta có pt:
\(\dfrac{x}{40}+\dfrac{x}{30}+0,5=9,25\)
\(\Leftrightarrow\dfrac{x}{40}+\dfrac{x}{30}=8,75\)
\(\Leftrightarrow70x=10500\)
\(\Leftrightarrow x=150\) (thỏa mãn đk)
Vậy quãng đường AB dài 150 km
Đổi 30' = \(\dfrac{1}{2}\) h; 9h15' = \(\dfrac{37}{4}\)
Gọi quãng đường AB là x km (x > 0)
Ta có: Thời gian người đó đi từ A đến B là \(\dfrac{x}{40}\)h
Thời gian người đó đi từ B về A là \(\dfrac{x}{30}\)h
Theo đề bài ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{2}=\dfrac{37}{4}\)
⇔ \(\dfrac{3x}{120}+\dfrac{4x}{120}+\dfrac{60}{120}=\dfrac{1110}{120}\)
⇔ 3x + 4x + 60 = 1110
⇔ 7x = 1110 - 60
⇔ 7x = 1050
⇔ x = 150 (thỏa mãn)
Vậy quãng đường AB dài 150 km

Gọi độ dài quãng đường AB là x
Thời gian đi là x/40(h)
Thời gian về là x/30(h)
Theo đề, ta có: x/40+x/30=8,75
hay x=150
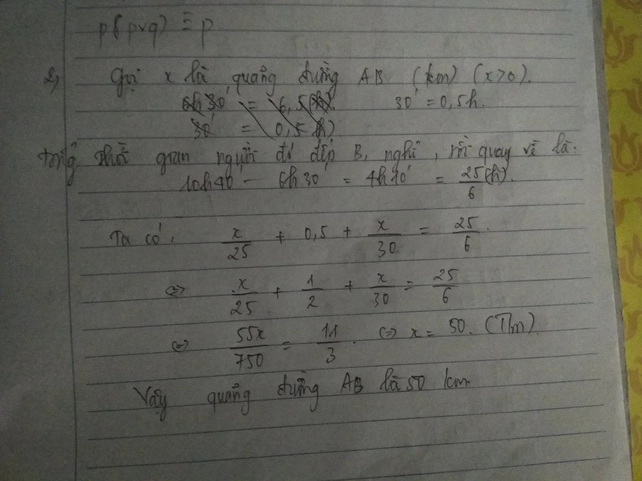 Good luck~
Good luck~
6h30p = 6,5 giờ
30p = 0,5 giờ
Gọi độ dài quãng đường AB là a(km)
Thời gian lúc đi là
\(\dfrac{a}{40}\left(h\right)\)
Thời gian lúc về
\(\dfrac{a}{30}\left(h\right)\)
Ta có
\(\dfrac{a}{30}+\dfrac{a}{40}=6,5-0,5\\ \Leftrightarrow\dfrac{7a}{120}=6\Leftrightarrow a\approx103\left(km\right)\)