Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi quãng đường AB là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{x}{30}+\dfrac{1}{2}+\dfrac{x}{40}=5+\dfrac{1}{6}\Rightarrow x=80\left(tm\right)\)

Đổi: 3 giờ 40 phút = \(\dfrac{11}{3}\) giờ; 10 phút = \(\dfrac{1}{6}\) giờ
Gọi độ dài quãng đường AB là x (km)
(ĐK: x > 0)
Thời gian xe máy đi từ A đến B là: \(\dfrac{x}{40}\) (giờ)
Thời gian xe máy đi từ B về A là: \(\dfrac{x}{30}\) (giờ)
Mà thời gian tổng cộng hết 11/3 giờ nên ta có pt:
\(\dfrac{x}{40}+\dfrac{1}{6}+\dfrac{x}{30}=\dfrac{11}{3}\\ \Leftrightarrow\dfrac{3x}{120}+\dfrac{20}{120}+\dfrac{4x}{120}=\dfrac{440}{120}\\ \Leftrightarrow3x+4x+20=440\\ \Leftrightarrow7x=420\\ \Leftrightarrow x=60\left(tmđk\right)\)
Vậy quãng đường AB dài 60km
Đổi \(3h40'=\dfrac{11}{3}h\)
\(10'=\dfrac{1}{6}h\)
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Thời gian xe máy đi từ A đến B là:
\(\dfrac{x}{40}\left(h\right)\)
Thời gian xe máy đi từ B về A là:
\(\dfrac{x}{30}\left(h\right)\)
Theo đề, ta có: \(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{6}=\dfrac{11}{3}\)
\(\Leftrightarrow\dfrac{3x}{120}+\dfrac{4x}{120}=\dfrac{11}{3}-\dfrac{1}{6}=\dfrac{21}{6}\)
\(\Leftrightarrow\dfrac{7x}{120}=\dfrac{7}{2}\)
\(\Leftrightarrow7x=420\)
hay x=60(thỏa ĐK)
Vậy: Độ dài quãng đường AB là 60km

10 phút = \(\dfrac{1}{6}\) giờ
6 giờ 40 phút = \(\dfrac{20}{3}\) (giờ)
Gọi x (km) là độ dài quãng đường AB (Điều kiện: x ∈ Z; x > 0)
Thời gian đi từ A đến B là \(\dfrac{x}{30}\) (giờ)
Thời gian đi từ B đến A là \(\dfrac{x}{35}\) (giờ)
Theo đề bài ta có phương trình:
\(\dfrac{x}{30}+\dfrac{x}{35}+\dfrac{1}{6}\) = \(\dfrac{20}{3}\)
MSC (mẫu số chung): 1050
Quy đồng mẫu hai vế và khử mẫu ta được:
35x + 30x + 175 = 7000
⇔ 35x + 30x = 7000 - 175
⇔ 65x = 6825
⇔ x = 105 (nhận)
Vậy quãng đường AB dài 105 km

Gọi độ dài AB là x
Theo đề, ta có: x/30+x/25+1/6=5+2/3
=>x=75
Lời giải:
Thời gian đi lần về (không tính thời gian nghỉ) là:
$5h40'-10'=5h30'=5,5h$
Thời gian đi: $\frac{AB}{30}$ (h)
Thời gian về: $\frac{AB}{25}$ (h)
Tổng thời gian đi và về: $\frac{AB}{30}+\frac{AB}{25}=5,5$
$\Leftrightarrow AB.\frac{11}{150}=5,5$
$\Rightarrow AB=75$ (km)

9h15p=9,25h
30p=0,5h
Gọi quãng đường AB là x (km) đk: x>0
Thời gian xe đi từ A đến B: \(\dfrac{x}{40}\)(h)
Thời gian xe đi từ B về A: \(\dfrac{x}{30}\)(h)
Theo bài, ta có pt:
\(\dfrac{x}{40}+\dfrac{x}{30}+0,5=9,25\)
\(\Leftrightarrow\dfrac{x}{40}+\dfrac{x}{30}=8,75\)
\(\Leftrightarrow70x=10500\)
\(\Leftrightarrow x=150\) (thỏa mãn đk)
Vậy quãng đường AB dài 150 km
Đổi 30' = \(\dfrac{1}{2}\) h; 9h15' = \(\dfrac{37}{4}\)
Gọi quãng đường AB là x km (x > 0)
Ta có: Thời gian người đó đi từ A đến B là \(\dfrac{x}{40}\)h
Thời gian người đó đi từ B về A là \(\dfrac{x}{30}\)h
Theo đề bài ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{1}{2}=\dfrac{37}{4}\)
⇔ \(\dfrac{3x}{120}+\dfrac{4x}{120}+\dfrac{60}{120}=\dfrac{1110}{120}\)
⇔ 3x + 4x + 60 = 1110
⇔ 7x = 1110 - 60
⇔ 7x = 1050
⇔ x = 150 (thỏa mãn)
Vậy quãng đường AB dài 150 km

Gọi độ dài quãng đường AB là x
Thời gian đi là x/40(h)
Thời gian về là x/30(h)
Theo đề, ta có: x/40+x/30=8,75
hay x=150

Đổi \(15phút=\dfrac{1}{4}\left(h\right);2giờ30phút=\dfrac{5}{2}\left(h\right)\)
Gọi quãng đường AB là \(x\left(km;x>0\right)\)
Thì Thời gian người đó đi từ đến B là \(\dfrac{x}{50}\left(h\right)\)
Thời gian người đó quay về A là : \(\dfrac{x}{40}\left(h\right)\)
Vì đến B người đó nghỉ lại \(\dfrac{1}{4}h\) và thời gian tổng cộng là \(\dfrac{5}{2}h\) nên ta có phương trình:
\(\dfrac{x}{40}+\dfrac{x}{50}+\dfrac{1}{4}=\dfrac{5}{2}\)
\(\Leftrightarrow5x+4x+50=500\)
\(\Leftrightarrow9x=450\)
\(\Leftrightarrow x=50\left(nhận\right)\)
Vậy độ dài quãng đường AB là \(50km\)
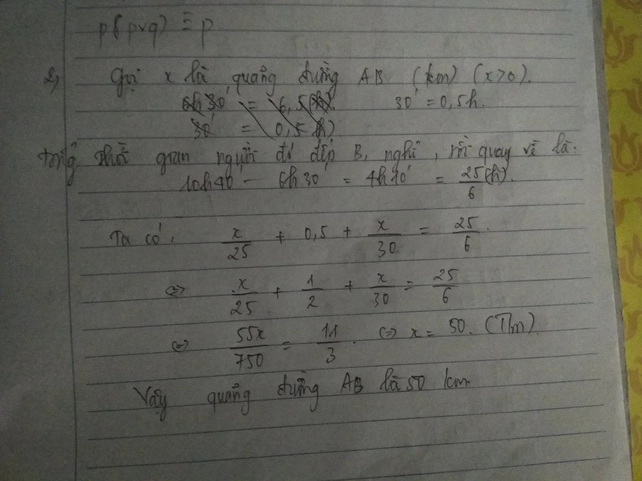 Good luck~
Good luck~

6h30p = 6,5 giờ
30p = 0,5 giờ
Gọi độ dài quãng đường AB là a(km)
Thời gian lúc đi là
\(\dfrac{a}{40}\left(h\right)\)
Thời gian lúc về
\(\dfrac{a}{30}\left(h\right)\)
Ta có
\(\dfrac{a}{30}+\dfrac{a}{40}=6,5-0,5\\ \Leftrightarrow\dfrac{7a}{120}=6\Leftrightarrow a\approx103\left(km\right)\)