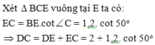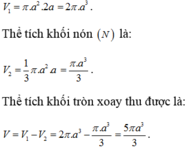Hình thang ABCD vuông tại A và D, AB=AD<CD, B(1;2), y=2 đường thẳng \(\Delta:7x-y-25=0\) cắt các đoạn AD,CD lần lượt tại M và N sao cho BM vuôn góc với BC, tia BN là tia phân giác trong góc MBC. Tìm tọa độ D biết D có hoành độ dương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
E
Etermintrude💫
15 tháng 3 2021
Đúng(1)
Những câu hỏi liên quan
10 tháng 12 2023
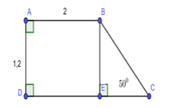
ABCD là hình thang vuông tại A và D
=>\(S_{ABCD}=\dfrac{1}{2}\cdot AD\cdot\left(BA+CD\right)=\dfrac{1}{2}\cdot8\cdot\left(12+18\right)=4\cdot30=120\left(cm^2\right)\)
Diện tích tam giác ABD là:
\(S_{ABD}=\dfrac{1}{2}\cdot AB\cdot AD=\dfrac{1}{2}\cdot12\cdot8=4\cdot12=48\left(cm^2\right)\)
Ta có: \(S_{ABD}+S_{BDC}=S_{ABCD}\)
=>\(S_{BDC}+48=120\)
=>\(S_{BDC}=72\left(cm^2\right)\)
=>\(\dfrac{S_{BCD}}{S_{ABCD}}=\dfrac{72}{120}=\dfrac{3}{5}=60\%\)
29 tháng 2 2024
Xét ΔMCD có AB//CD
nên ΔMAB~ΔMDC
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot S_{MDC}\)
Ta có: \(S_{MAB}+S_{ABCD}=S_{MDC}\)
=>\(S_{ABCD}=S_{MDC}-\dfrac{1}{9}\cdot S_{MDC}=\dfrac{8}{9}\cdot S_{MDC}\)
=>\(S_{MDC}=64:\dfrac{8}{9}=72\left(cm^2\right)\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot72=8\left(cm^2\right)\)
CM
20 tháng 6 2019
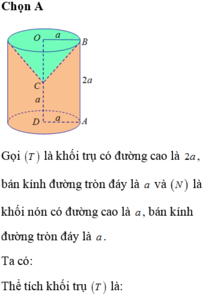
Chọn đáp án A
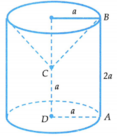
Gọi (T) là khối trụ có đường cao là 2a, bán kính đường tròn đáy là a và (N) là khối nón có đường cao là a, bán kính đường tròn đáy là a
CM
24 tháng 11 2019
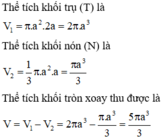
Đáp án A
Gọi V là thể tích của khối tròn xoay cần tính, khi đó V = V 1 − V 2 với
V1 là thể tích khối trụ có chiều cao h 1 = A B , bán kính R = A D → V 1 = π R 2 h 1 = 2 π a 3
V 2 là thể tích khối trụ có chiều cao h 1 = A B − C D , bán kính R = A D → V 2 = 1 3 π r 2 h 2 = π a 3 3
Vậy thể tích cần tính là V = V 1 − V 2 = 2 π a 3 − π a 3 3 = 5 π a 3 3
