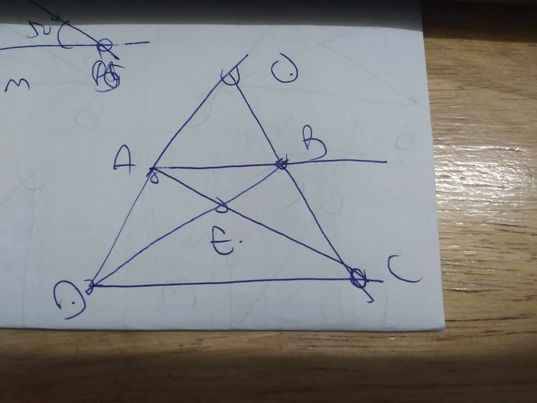
Vẽ hình hộ mình lun nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Ta có: BM+DB=DM
CM+CE=ME
mà BM=CM
và DB=CE
nên DM=ME
hay M là trung điểm của DE
Ta có: ΔADE cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
c: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK và AH=AK
d: Xét ΔADE có
AH/AD=AK/AE
nên HK//DE

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH

Bài 2:
Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2=5(cm)

A B H C D
Bài 1:
a) Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC^2=8^2+6^2\)
\(\Rightarrow BC^2=64\)
\(\Rightarrow BC=8cm\)
Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\)
\(\Rightarrow AH=4,8cm\)
Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(AB^2=BH.BC\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\Rightarrow CH=BC-BH=10cm-3,6cm=6,4cm\)
b) Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) và \(\Delta ADH\left(\widehat{H}=90^o\right)\) có:
\(BH=HD\) (giả thiết)
\(AH\) là cạnh chung
\(\Rightarrow\Delta ABH=\Delta ADH\left(cgv.cgv\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ADH}\) (\(2\) cạnh tương ứng)

a, Vì MA là tiếp tuyến (O) với A là tiếp điểm
=> ^MAO = 900
I là trung điểm BC => OI vuông BC
Xét tứ giác MAOI có
^MAO + MIO = 1800
mà 2 góc này đối
Vậy tứ giác MAOI là tứ giác nt 1 đường tròn
b, Xét tam giác MAB và tam giác MCA có
^M _ chung
^MAB = ^MCA ( cùng chắn cung AB )
Vậy tam giác MAB ~ tam giác MCA (g.g)
\(\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)(1)
Xét tam giác MAO vuông tại A, đường cao AH
Ta có AM^2 = MH.MO ( tỉ lệ thức ) (2)
Xét tam giác MHK và tam giác MIO có
^M _ chung
^MHK = ^MIO = 900
Vậy tam giác MHK ~ tam giác MIO (g,g)
\(\dfrac{MH}{MI}=\dfrac{MK}{MO}\Rightarrow MH.MO=MK.MI\)(3)
Từ (1) ; (2) ; (3) suy ra \(MK.MI=MB.MC\)

Vì hai góc xOz và góc zOy là hai góc kề bù mà xOz = 120 độ vậy zOy = 180 - 120 = 60 độ
Gỉa sử tia Ot là tia phân giác của góc zOy thì yOt = zOy/2 = 60/2 = 30độ. Vậy tia Om trùng với tia phân giác của góc zOy nên Om là tia phân giác của góc zOy
Hai góc yOz và xOz" bằng nhau vì đối đỉnh đó.
nhớ cho mình một đúng nhé





a, Xét tam giác EAB có : AE = AB (gt)
Vậy tam giác EAB cân tại A
b, Vì EA = AC ; EA = AB
=> AB = AC Xét tam giác ABC có AB = AC (cmt)
Vậy tam giác ABC cân tại A
=> AD là phân giác đồng thời là đường cao
=> AD vuông BC (1)
Vì AB = EA = AC
=> tam giác EBC vuông tại B => EB vuông BC (2)
Từ (1) ; (2) suy ra AD//EB
c, Ta có : ^AEB = ^ABE ( vì tam giác EAB cân tại A )
Lại có : ^EAB = ^BAD ( soletrong do AD//EB )
mà AD là phân giác ^BAC = 2^BAD
=> ^BAC = 2^AEB
dòng 2 c bạn sửa hộ mình ^EBA = ^BAD ( soletrong do AD // EB )