
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét tam giác EAB có : AE = AB (gt)
Vậy tam giác EAB cân tại A
b, Vì EA = AC ; EA = AB
=> AB = AC Xét tam giác ABC có AB = AC (cmt)
Vậy tam giác ABC cân tại A
=> AD là phân giác đồng thời là đường cao
=> AD vuông BC (1)
Vì AB = EA = AC
=> tam giác EBC vuông tại B => EB vuông BC (2)
Từ (1) ; (2) suy ra AD//EB
c, Ta có : ^AEB = ^ABE ( vì tam giác EAB cân tại A )
Lại có : ^EAB = ^BAD ( soletrong do AD//EB )
mà AD là phân giác ^BAC = 2^BAD
=> ^BAC = 2^AEB
dòng 2 c bạn sửa hộ mình ^EBA = ^BAD ( soletrong do AD // EB )

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH

A B H C D
Bài 1:
a) Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC^2=8^2+6^2\)
\(\Rightarrow BC^2=64\)
\(\Rightarrow BC=8cm\)
Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\)
\(\Rightarrow AH=4,8cm\)
Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(AB^2=BH.BC\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\Rightarrow CH=BC-BH=10cm-3,6cm=6,4cm\)
b) Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) và \(\Delta ADH\left(\widehat{H}=90^o\right)\) có:
\(BH=HD\) (giả thiết)
\(AH\) là cạnh chung
\(\Rightarrow\Delta ABH=\Delta ADH\left(cgv.cgv\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ADH}\) (\(2\) cạnh tương ứng)

a: \(\widehat{EKI}+\widehat{KEI}=90^0\)
\(\widehat{IDK}+\widehat{KEI}=90^0\)
Do đó: \(\widehat{EKI}=\widehat{IDK}\)
b: \(\widehat{KED}+\widehat{F}=90^0\)
\(\widehat{KDF}+\widehat{F}=90^0\)
Do đó: \(\widehat{KED}=\widehat{KDF}\)


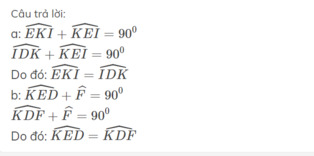



a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Ta có: BM+DB=DM
CM+CE=ME
mà BM=CM
và DB=CE
nên DM=ME
hay M là trung điểm của DE
Ta có: ΔADE cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
c: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK và AH=AK
d: Xét ΔADE có
AH/AD=AK/AE
nên HK//DE