Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{HAC}+\widehat{C}=90^0\)
\(\widehat{EHC}+\widehat{C}=90^0\)
Do đó: \(\widehat{HAC}=\widehat{EHC}\)
b: \(\widehat{BAH}+\widehat{B}=90^0\)
\(\widehat{ACH}+\widehat{B}=90^0\)
Do đó: \(\widehat{BAH}=\widehat{ACH}\)

a) BD; CE là đường cao => tam giác ABD và tam giác ACE vuông : có: AB = AC (do tam giác ABC cân tại A ); góc A chung
=> tam giác ABD = ACE (cạnh huyền - góc nhọn )
b) Tam giác BDC vuông tại D có trung tuyến DH ứng với cạnh huyền BC => DH = HC = BC/ 2
=> tam giác HDC cân tại H
c) sửa đề: chứng minh: DM = MC
Tam giác DHC cân tại H có HM là đuơng cao nên đông thời là đường trung tuyến => M là TĐ của DC=> DM = MC
d) Tam giác HND vuông tại M có: MI là trung tuyến => MI = HI = HD/2
=> tam giác IHM cân tại I => góc IHM = IMH
lại có HM là p/g của góc DHC => góc IHM = MHC
=> góc IMH = MHC mà 2 góc này ở vị trí SLT => MI // HC mà HC vuông góc với AH
=> MI vuông góc với AH
bạn Nobita Kun giải bài không theo điểm như đề bài cho, ý c đề bài đúng rồi ạ. ý d thì bạn hiểu nhầm đề rồi, bạn xem lại điểm I nhé

Karroy Yi !! pài làm của pn nè!!!
a) Tứ giác KDHA có
DKA=90 (DK vuông góc với AB)
A =90 (gt) , DHA=90 (DH vuông góc với AC)
=>KDHA là hcn =>KDH=90 (độ) (đpcm)
b) KDHA là hcn có pân giác AD =>KDHA là h vuông
=>DH=DK
Ta có : DEC+ECD=90 (Tam giác DCE vuông tại D)
ECD+KBD=90 (Tam giác ABC vuông tại A)
=>DEC=KBD
Mặt khác : KBD+BDK=90 (Tam giác BDK vuông tại K)
DEC+EDH=90 ( Tam giác DEH vuông tại H)
=>BDK=EDH
Xét tam giác vuông BKD và tam giác vuông EHD có:
DH=DK (cmt)
BDK=EDH (cmt)
=> \(\Delta\) vuông BKD=\(\Delta\) vuông EHD ( Cạnh góc vuông- góc nhọn )
=>DB=DE (2 cạnh tương ứng )
................đpcm
**** mk naaaaaaaaaa!!!
Vẽ hình ở chỗ nào đây ? Mình có thấy chỗ nào vẽ hình đâu ? Mình kiếm trên câu trả lời thì chả thấy có chỗ nào vẽ hình cả . Nên mình không biết vẽ hình .
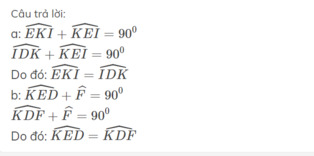



a: \(\widehat{EKI}+\widehat{KEI}=90^0\)
\(\widehat{IDK}+\widehat{KEI}=90^0\)
Do đó: \(\widehat{EKI}=\widehat{IDK}\)
b: \(\widehat{KED}+\widehat{F}=90^0\)
\(\widehat{KDF}+\widehat{F}=90^0\)
Do đó: \(\widehat{KED}=\widehat{KDF}\)